Quantum Supremacy in Tomographic Imaging: Advances in Quantum Tomography Algorithms

Quantum computing has emerged as a transformative paradigm, capable of tackling complex computational problems that are infeasible for classical methods within a practical timeframe. At the core of this advancement lies the concept of quantum supremacy, which signifies the ability of quantum processors to surpass classical systems in specific tasks. In the context of tomographic image reconstruction, quantum optimization algorithms enable faster processing and clearer imaging than conventional methods. This study further substantiates quantum supremacy by reducing the required projection angles for tomographic reconstruction while enhancing robustness against image artifacts. Notably, our experiments demonstrated that the proposed algorithm accurately reconstructed tomographic images without artifacts, even when up to 50% error was introduced into the sinogram to induce ring artifacts. Furthermore, it achieved precise reconstructions using only 50% of the projection angles from the original sinogram spanning 0{\deg} to 180{\deg}. These findings highlight the potential of quantum algorithms to revolutionize tomographic imaging by enabling efficient and accurate reconstructions under challenging conditions, paving the way for broader applications in medical imaging, material science, and advanced tomography systems as quantum computing technologies continue to advance.

Quantum optimization algorithms for CT image segmentation from X-ray data

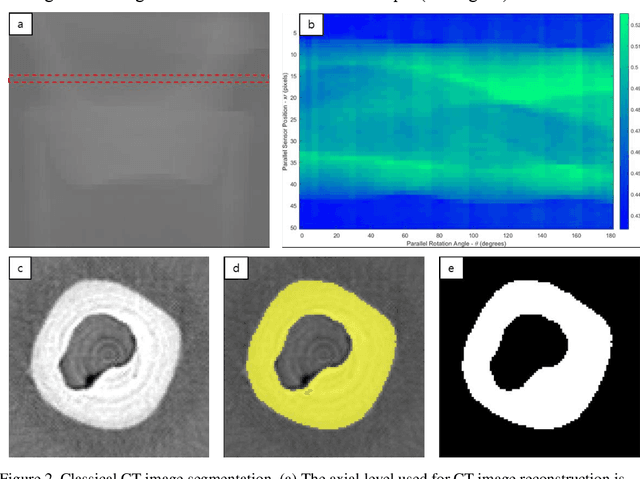
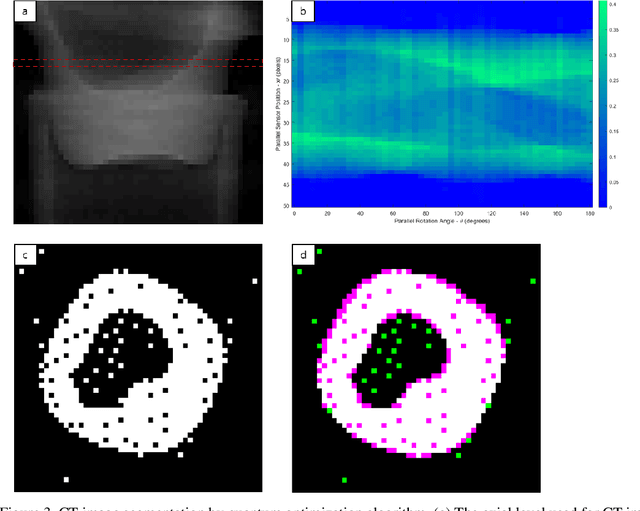
Computed tomography (CT) is an important imaging technique used in medical analysis of the internal structure of the human body. Previously, image segmentation methods were required after acquiring reconstructed CT images to obtain segmented CT images which made it susceptible to errors from both reconstruction and segmentation algorithms. However, this paper introduces a new approach using an advanced quantum optimization algorithm called quadratic unconstrained binary optimization (QUBO). This algorithm enables acquisition of segmented CT images from X-ray projection data with minimized discrepancies between experimentally obtained sinograms and quantized sinograms derived from quantized segmented CT images using the Radon transform. This study utilized D-Wave's hybrid solver system for verification on real-world X-ray data.

Highly accurate quantum optimization algorithm for CT image reconstructions based on sinogram patterns

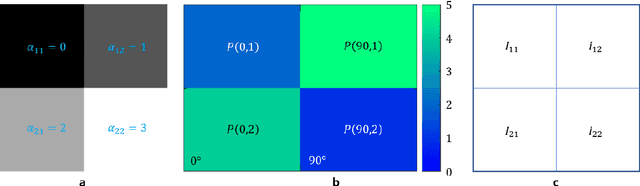
Computed tomography has been developed as a non-destructive technique for observing internal images of samples. It was difficult to obtain a clean CT image due to various artifacts generated during scanning and limitations of backprojection. Recently, an iterative optimization algorithm has been developed that uses the entire sinogram to make small errors in various artifacts. In this paper, we introduce a method of representing CT images using a combination of qubits. Each qubit variable can represent the internal structure of a real sample by energy optimization. We tested simple image samples in a quantum annealer and a gated model quantum computer.

Noise-resistant reconstruction algorithm based on the sinogram pattern

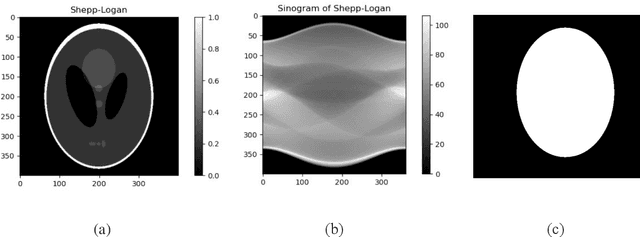
We introduce a new CT image reconstruction algorithm that is less affected by various artifacts. The new reconstruction algorithm is a method of minimizing the difference between synchrotron X-ray tomography data and sinograms generated using Radon transform of CT images. The CT image is iteratively updated to reduce the difference from the sinogram of the data. This method can obtain clean CT images from the projection data, which can create ring artifacts or metal artifacts. Also, even if the sample size is larger than the CCD and/or the projection image does not satisfy the Beer-Lambert law, a clean CT image can be reconstructed. Our new reconstruction algorithm can also be applied to fan beam CT or cone beam CT