Koya Sato
Mitigating the Impact of Location Uncertainty on Radio Map-Based Predictive Rate Selection via Noisy-Input Gaussian Process
Sep 18, 2025Abstract:This paper proposes a predictive rate-selection framework based on Gaussian process (GP)-based radio map construction that is robust to location uncertainty. Radio maps are a promising tool for improving communication efficiency in 6G networks. Although they enable the design of location-based maximum transmission rates by exploiting statistical channel information, existing discussions often assume perfect (i.e., noiseless) location information during channel sensing. Since such information must be obtained from positioning systems such as global navigation satellite systems, it inevitably involves positioning errors; this location uncertainty can degrade the reliability of radio map-based wireless systems. To mitigate this issue, we introduce the noisy-input GP (NIGP), which treats location noise as additional output noise by applying a Taylor approximation of the function of interest. Numerical results demonstrate that the proposed NIGP-based design achieves more reliable transmission-rate selection than pure GP and yields higher throughput than path loss-based rate selection.
Adaptively Weighted Averaging Over-the-Air Computation and Its Application to Distributed Gaussian Process Regression
Jan 29, 2025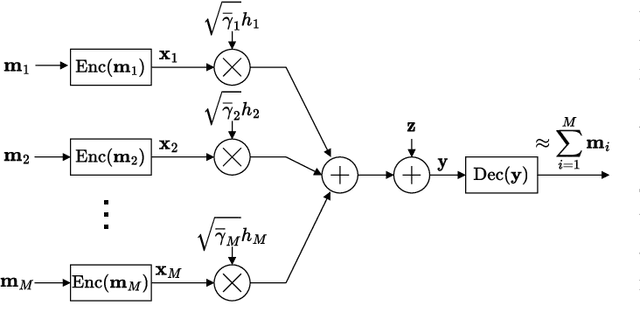
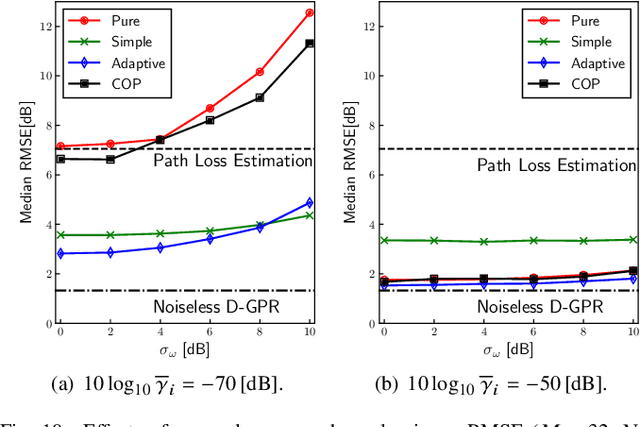
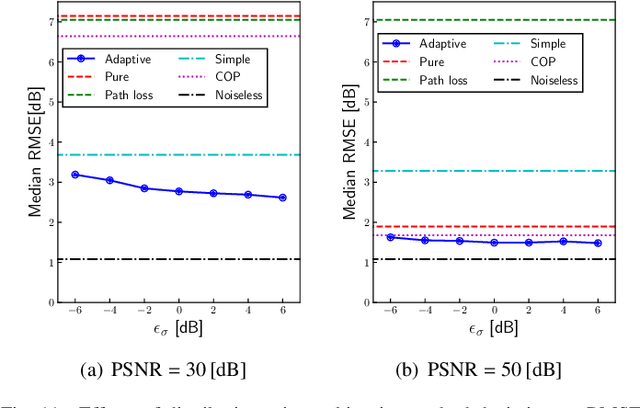
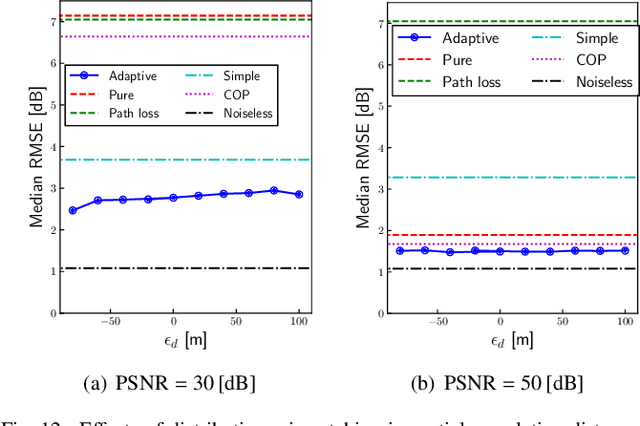
Abstract:This paper introduces a noise-tolerant computing method for over-the-air computation (AirComp) aimed at weighted averaging, which is critical in various Internet of Things (IoT) applications such as environmental monitoring. Traditional AirComp approaches, while efficient, suffer significantly in accuracy due to noise enhancement in the normalization by the sum of weights. Our proposed method allows nodes to adaptively truncate their weights based on the channel conditions, thereby enhancing noise tolerance. Applied to distributed Gaussian process regression, the method facilitates low-latency, low-complexity, and high-accuracy distributed regression across a range of signal-to-noise ratios. We evaluate the performance of the proposed method in a radio map construction problem, which is a task for visualizing the radio environment based on limited sensing information and spatial interpolation. Numerical results demonstrate that our approach not only maintains computational accuracy in high noise scenarios but also achieves performance close to ideal conditions in high SNR environments. This advancement holds significant implications for the deployment of real-time, large-scale IoT systems, providing a scalable solution to enhance reliability and efficiency in data-driven environmental monitoring.
Over-the-Air Gaussian Process Regression Based on Product of Experts
Oct 06, 2022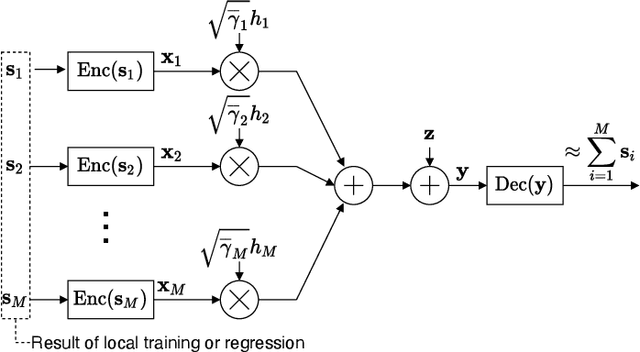
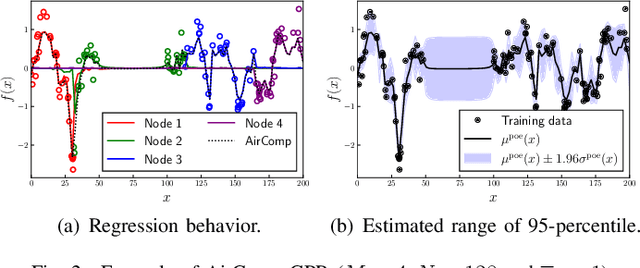

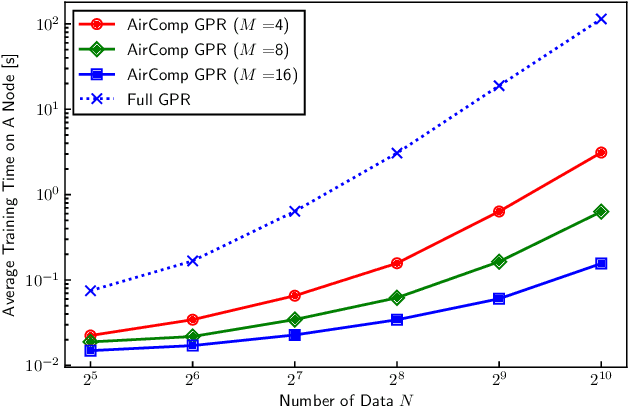
Abstract:This paper proposes a distributed Gaussian process regression (GPR) with over-the-air computation, termed AirComp GPR, for communication- and computation-efficient data analysis over wireless networks. GPR is a non-parametric regression method that can model the target flexibly. However, its computational complexity and communication efficiency tend to be significant as the number of data increases. AirComp GPR focuses on that product-of-experts-based GPR approximates the exact GPR by a sum of values reported from distributed nodes. We introduce AirComp for the training and prediction steps to allow the nodes to transmit their local computation results simultaneously; the communication strategies are presented, including distributed training based on perfect and statistical channel state information cases. Applying to a radio map construction task, we demonstrate that AirComp GPR speeds up the computation time while maintaining the communication cost in training constant regardless of the numbers of data and nodes.
Network-Density-Controlled Decentralized Parallel Stochastic Gradient Descent in Wireless Systems
Feb 25, 2020


Abstract:This paper proposes a communication strategy for decentralized learning on wireless systems. Our discussion is based on the decentralized parallel stochastic gradient descent (D-PSGD), which is one of the state-of-the-art algorithms for decentralized learning. The main contribution of this paper is to raise a novel open question for decentralized learning on wireless systems: there is a possibility that the density of a network topology significantly influences the runtime performance of D-PSGD. In general, it is difficult to guarantee delay-free communications without any communication deterioration in real wireless network systems because of path loss and multi-path fading. These factors significantly degrade the runtime performance of D-PSGD. To alleviate such problems, we first analyze the runtime performance of D-PSGD by considering real wireless systems. This analysis yields the key insights that dense network topology (1) does not significantly gain the training accuracy of D-PSGD compared to sparse one, and (2) strongly degrades the runtime performance because this setting generally requires to utilize a low-rate transmission. Based on these findings, we propose a novel communication strategy, in which each node estimates optimal transmission rates such that communication time during the D-PSGD optimization is minimized under the constraint of network density, which is characterized by radio propagation property. The proposed strategy enables to improve the runtime performance of D-PSGD in wireless systems. Numerical simulations reveal that the proposed strategy is capable of enhancing the runtime performance of D-PSGD.
DyANE: Dynamics-aware node embedding for temporal networks
Sep 12, 2019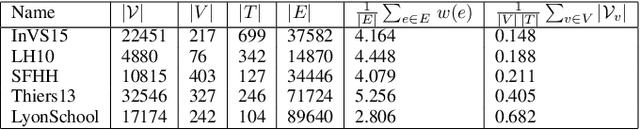
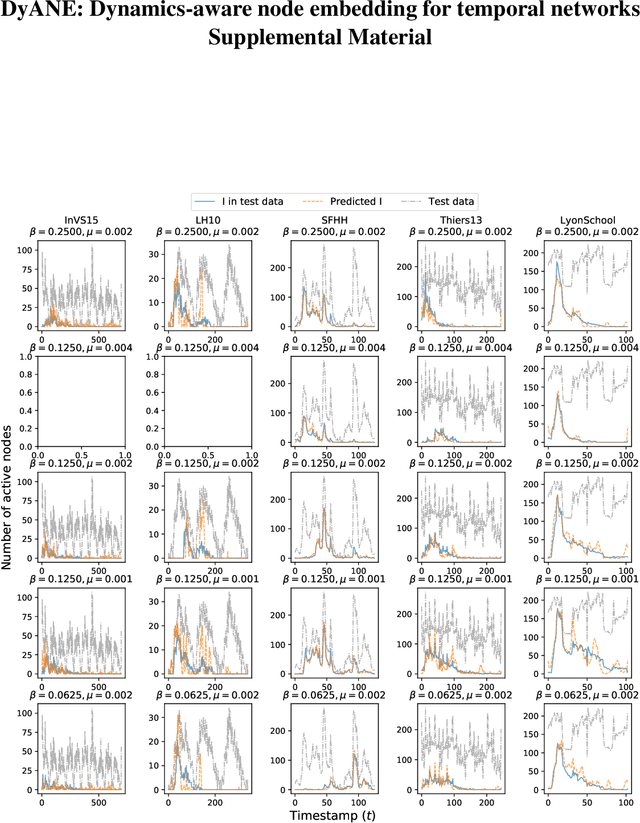

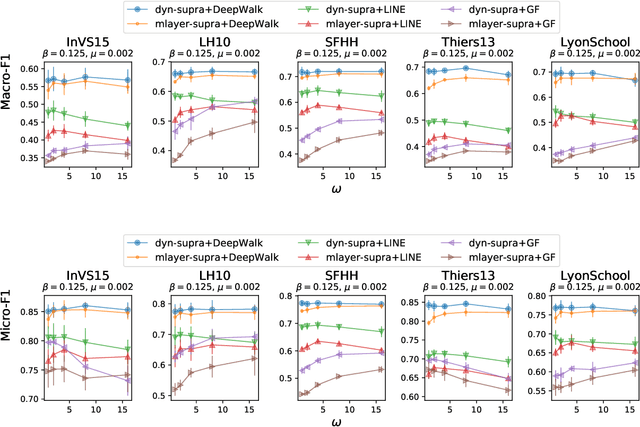
Abstract:Low-dimensional vector representations of network nodes have proven successful to feed graph data to machine learning algorithms and to improve performance across diverse tasks. Most of the embedding techniques, however, have been developed with the goal of achieving dense, low-dimensional encoding of network structure and patterns. Here, we present a node embedding technique aimed at providing low-dimensional feature vectors that are informative of dynamical processes occurring over temporal networks - rather than of the network structure itself - with the goal of enabling prediction tasks related to the evolution and outcome of these processes. We achieve this by using a modified supra-adjacency representation of temporal networks and building on standard embedding techniques for static graphs based on random-walks. We show that the resulting embedding vectors are useful for prediction tasks related to paradigmatic dynamical processes, namely epidemic spreading over empirical temporal networks. In particular, we illustrate the performance of our approach for the prediction of nodes' epidemic states in a single instance of the spreading process. We show how framing this task as a supervised multi-label classification task on the embedding vectors allows us to estimate the temporal evolution of the entire system from a partial sampling of nodes at random times, with potential impact for nowcasting infectious disease dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge