Entrenchment Relations: A Uniform Approach to Nonmonotonicity

We show that Gabbay's nonmonotonic consequence relations can be reduced to a new family of relations, called entrenchment relations. Entrenchment relations provide a direct generalization of epistemic entrenchment and expectation ordering introduced by Gardenfors and Makinson for the study of belief revision and expectation inference, respectively.

Ordering-based Representations of Rational Inference

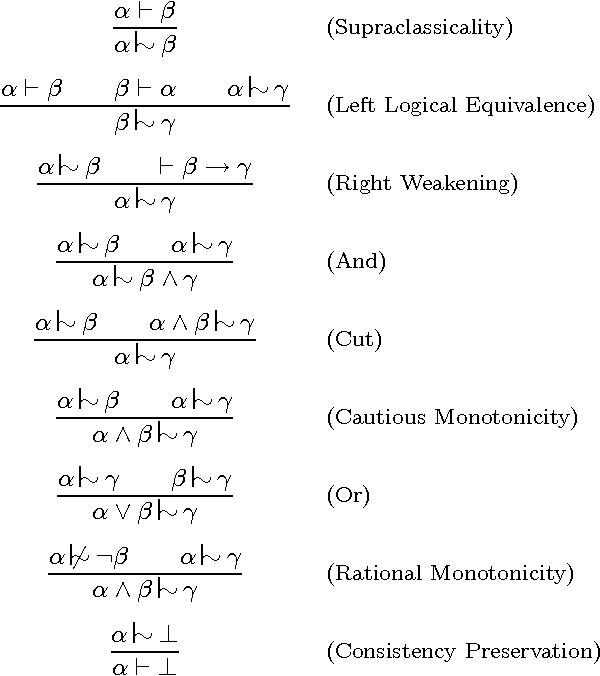
Rational inference relations were introduced by Lehmann and Magidor as the ideal systems for drawing conclusions from a conditional base. However, there has been no simple characterization of these relations, other than its original representation by preferential models. In this paper, we shall characterize them with a class of total preorders of formulas by improving and extending Gardenfors and Makinson's results for expectation inference relations. A second representation is application-oriented and is obtained by considering a class of consequence operators that grade sets of defaults according to our reliance on them. The finitary fragment of this class of consequence operators has been employed by recent default logic formalisms based on maxiconsistency.

Modal Logics for Topological Spaces

In this thesis we shall present two logical systems, MP and MP, for the purpose of reasoning about knowledge and effort. These logical systems will be interpreted in a spatial context and therefore, the abstract concepts of knowledge and effort will be defined by concrete mathematical concepts.

To Preference via Entrenchment

We introduce a simple generalization of Gardenfors and Makinson's epistemic entrenchment called partial entrenchment. We show that preferential inference can be generated as the sceptical counterpart of an inference mechanism defined directly on partial entrenchment.

Knowledge on Treelike Spaces

This paper presents a bimodal logic for reasoning about knowledge during knowledge acquisition. One of the modalities represents (effort during) non-deterministic time and the other represents knowledge. The semantics of this logic are tree-like spaces which are a generalization of semantics used for modeling branching time and historical necessity. A finite system of axiom schemes is shown to be canonically complete for the formentioned spaces. A characterization of the satisfaction relation implies the small model property and decidability for this system.

Relevance Sensitive Non-Monotonic Inference on Belief Sequences

We present a method for relevance sensitive non-monotonic inference from belief sequences which incorporates insights pertaining to prioritized inference and relevance sensitive, inconsistency tolerant belief revision. Our model uses a finite, logically open sequence of propositional formulas as a representation for beliefs and defines a notion of inference from maxiconsistent subsets of formulas guided by two orderings: a temporal sequencing and an ordering based on relevance relations between the conclusion and formulas in the sequence. The relevance relations are ternary (using context as a parameter) as opposed to standard binary axiomatizations. The inference operation thus defined easily handles iterated revision by maintaining a revision history, blocks the derivation of inconsistent answers from a possibly inconsistent sequence and maintains the distinction between explicit and implicit beliefs. In doing so, it provides a finitely presented formalism and a plausible model of reasoning for automated agents.