Ordering-based Representations of Rational Inference
Paper and Code
Jul 26, 2000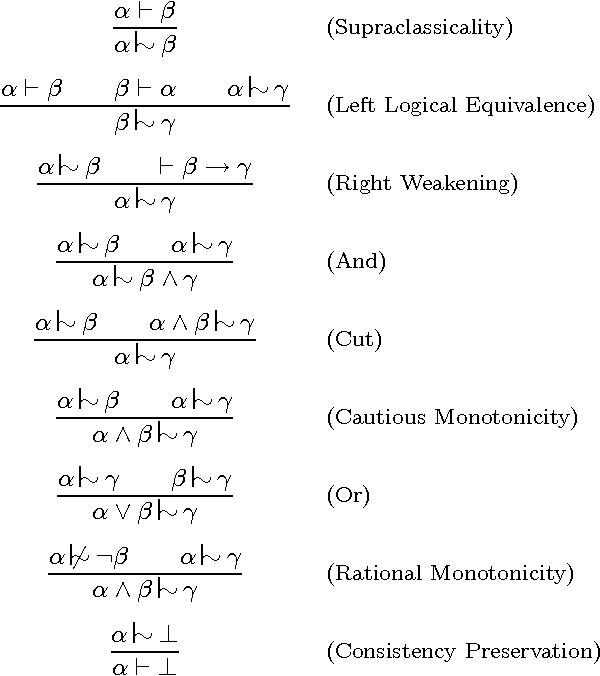
Rational inference relations were introduced by Lehmann and Magidor as the ideal systems for drawing conclusions from a conditional base. However, there has been no simple characterization of these relations, other than its original representation by preferential models. In this paper, we shall characterize them with a class of total preorders of formulas by improving and extending Gardenfors and Makinson's results for expectation inference relations. A second representation is application-oriented and is obtained by considering a class of consequence operators that grade sets of defaults according to our reliance on them. The finitary fragment of this class of consequence operators has been employed by recent default logic formalisms based on maxiconsistency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge