SpACNN-LDVAE: Spatial Attention Convolutional Latent Dirichlet Variational Autoencoder for Hyperspectral Pixel Unmixing

The Hyperspectral Unxming problem is to find the pure spectral signal of the underlying materials (endmembers) and their proportions (abundances). The proposed method builds upon the recently proposed method, Latent Dirichlet Variational Autoencoder (LDVAE). It assumes that abundances can be encoded as Dirichlet Distributions while mixed pixels and endmembers are represented by Multivariate Normal Distributions. However, LDVAE does not leverage spatial information present in an HSI; we propose an Isotropic CNN encoder with spatial attention to solve the hyperspectral unmixing problem. We evaluated our model on Samson, Hydice Urban, Cuprite, and OnTech-HSI-Syn-21 datasets. Our model also leverages the transfer learning paradigm for Cuprite Dataset, where we train the model on synthetic data and evaluate it on real-world data. We are able to observe the improvement in the results for the endmember extraction and abundance estimation by incorporating the spatial information. Code can be found at https://github.com/faisalqureshi/cnn-ldvae

Evaluation of Dirichlet Process Gaussian Mixtures for Segmentation on Noisy Hyperspectral Images

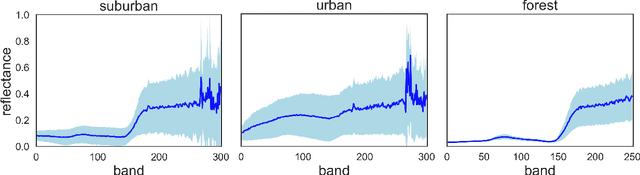
Image segmentation is a fundamental step for the interpretation of Remote Sensing Images. Clustering or segmentation methods usually precede the classification task and are used as support tools for manual labeling. The most common algorithms, such as k-means, mean-shift, and MRS, require an extra manual step to find the scale parameter. The segmentation results are severely affected if the parameters are not correctly tuned and diverge from the optimal values. Additionally, the search for the optimal scale is a costly task, as it requires a comprehensive hyper-parameter search. This paper proposes and evaluates a method for segmentation of Hyperspectral Images using the Dirichlet Process Gaussian Mixture Model. Our model can self-regulate the parameters until it finds the optimal values of scale and the number of clusters in a given dataset. The results demonstrate the potential of our method to find objects in a Hyperspectral Image while bypassing the burden of manual search of the optimal parameters. In addition, our model also produces similar results on noisy datasets, while previous research usually required a pre-processing task for noise reduction and spectral smoothing.

Hyperspectral Pixel Unmixing with Latent Dirichlet Variational Autoencoder

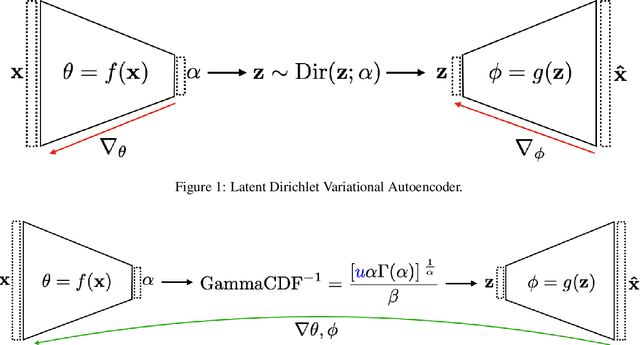
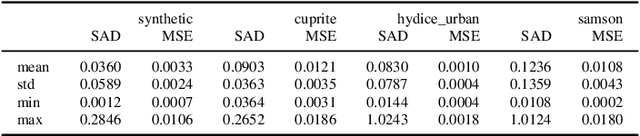
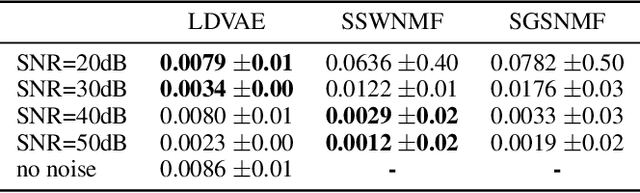
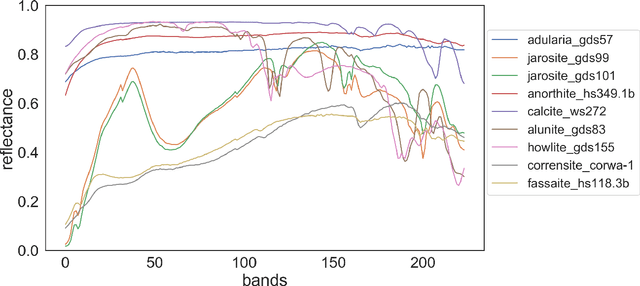
Hyperspectral pixel intensities result from a mixing of reflectances from several materials. This paper develops a method of hyperspectral pixel {\it unmixing} that aims to recover the "pure" spectral signal of each material (hereafter referred to as {\it endmembers}) together with the mixing ratios ({\it abundances}) given the spectrum of a single pixel. The unmixing problem is particularly relevant in the case of low-resolution hyperspectral images captured in a remote sensing setting, where individual pixels can cover large regions of the scene. Under the assumptions that (1) a multivariate Normal distribution can represent the spectra of an endmember and (2) a Dirichlet distribution can encode abundances of different endmembers, we develop a Latent Dirichlet Variational Autoencoder for hyperspectral pixel unmixing. Our approach achieves state-of-the-art results on standard benchmarks and on synthetic data generated using United States Geological Survey spectral library.

A study on the effects of compression on hyperspectral image classification

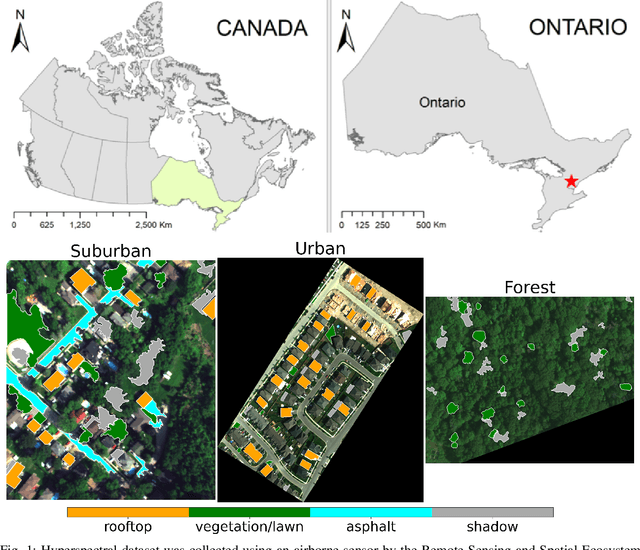
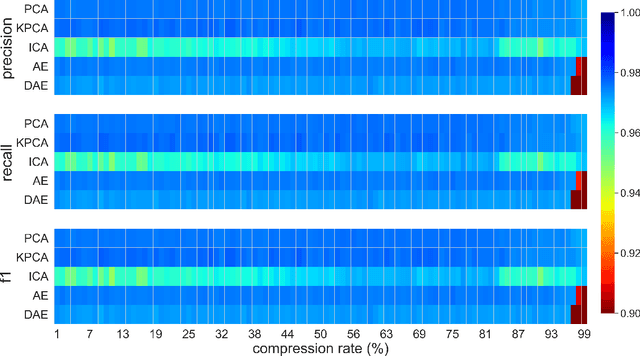
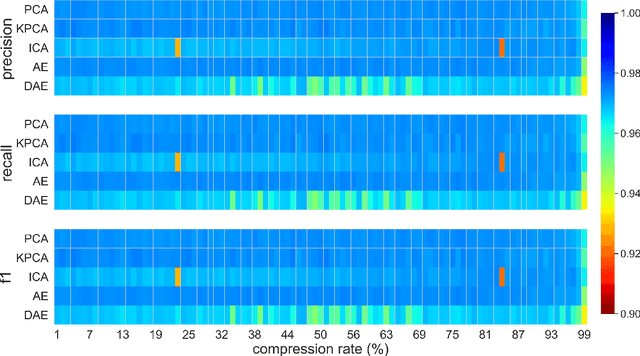
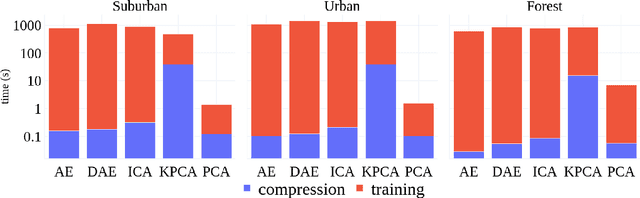
This paper presents a systematic study the effects of compression on hyperspectral pixel classification task. We use five dimensionality reduction methods -- PCA, KPCA, ICA, AE, and DAE -- to compress 301-dimensional hyperspectral pixels. Compressed pixels are subsequently used to perform pixel-based classifications. Pixel classification accuracies together with compression method, compression rates, and reconstruction errors provide a new lens to study the suitability of a compression method for the task of pixel-based classification. We use three high-resolution hyperspectral image datasets, representing three common landscape units (i.e. urban, transitional suburban, and forests) collected by the Remote Sensing and Spatial Ecosystem Modeling laboratory of the University of Toronto. We found that PCA, KPCA, and ICA post greater signal reconstruction capability; however, when compression rate is more than 90\% those methods showed lower classification scores. AE and DAE methods post better classification accuracy at 95\% compression rate, however decreasing again at 97\%, suggesting a sweet-spot at the 95\% mark. Our results demonstrate that the choice of a compression method with the compression rate are important considerations when designing a hyperspectral image classification pipeline.