Quasimetric Value Functions with Dense Rewards

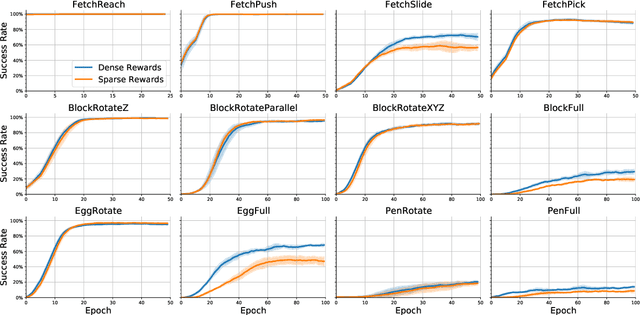
As a generalization of reinforcement learning (RL) to parametrizable goals, goal conditioned RL (GCRL) has a broad range of applications, particularly in challenging tasks in robotics. Recent work has established that the optimal value function of GCRL $Q^\ast(s,a,g)$ has a quasimetric structure, leading to targetted neural architectures that respect such structure. However, the relevant analyses assume a sparse reward setting -- a known aggravating factor to sample complexity. We show that the key property underpinning a quasimetric, viz., the triangle inequality, is preserved under a dense reward setting as well. Contrary to earlier findings where dense rewards were shown to be detrimental to GCRL, we identify the key condition necessary for triangle inequality. Dense reward functions that satisfy this condition can only improve, never worsen, sample complexity. This opens up opportunities to train efficient neural architectures with dense rewards, compounding their benefits to sample complexity. We evaluate this proposal in 12 standard benchmark environments in GCRL featuring challenging continuous control tasks. Our empirical results confirm that training a quasimetric value function in our dense reward setting indeed outperforms training with sparse rewards.