Kevin Christian Wibisono
Exponential Family Attention
Jan 28, 2025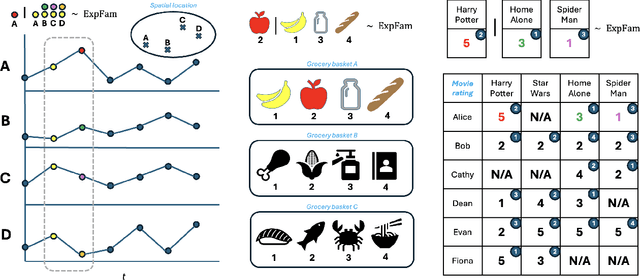

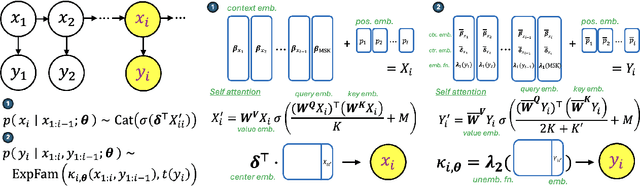
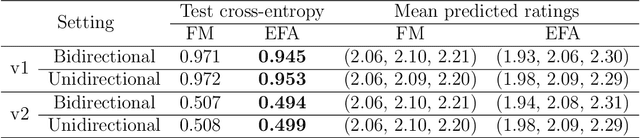
Abstract:The self-attention mechanism is the backbone of the transformer neural network underlying most large language models. It can capture complex word patterns and long-range dependencies in natural language. This paper introduces exponential family attention (EFA), a probabilistic generative model that extends self-attention to handle high-dimensional sequence, spatial, or spatial-temporal data of mixed data types, including both discrete and continuous observations. The key idea of EFA is to model each observation conditional on all other existing observations, called the context, whose relevance is learned in a data-driven way via an attention-based latent factor model. In particular, unlike static latent embeddings, EFA uses the self-attention mechanism to capture dynamic interactions in the context, where the relevance of each context observations depends on other observations. We establish an identifiability result and provide a generalization guarantee on excess loss for EFA. Across real-world and synthetic data sets -- including U.S. city temperatures, Instacart shopping baskets, and MovieLens ratings -- we find that EFA consistently outperforms existing models in capturing complex latent structures and reconstructing held-out data.
How In-Context Learning Emerges from Training on Unstructured Data: On the Role of Co-Occurrence, Positional Information, and Noise Structures
May 31, 2024Abstract:Large language models (LLMs) like transformers have impressive in-context learning (ICL) capabilities; they can generate predictions for new queries based on input-output sequences in prompts without parameter updates. While many theories have attempted to explain ICL, they often focus on structured training data similar to ICL tasks, such as regression. In practice, however, these models are trained in an unsupervised manner on unstructured text data, which bears little resemblance to ICL tasks. To this end, we investigate how ICL emerges from unsupervised training on unstructured data. The key observation is that ICL can arise simply by modeling co-occurrence information using classical language models like continuous bag of words (CBOW), which we theoretically prove and empirically validate. Furthermore, we establish the necessity of positional information and noise structure to generalize ICL to unseen data. Finally, we present instances where ICL fails and provide theoretical explanations; they suggest that the ICL ability of LLMs to identify certain tasks can be sensitive to the structure of the training data.
Bidirectional Attention as a Mixture of Continuous Word Experts
Jul 08, 2023Abstract:Bidirectional attention $\unicode{x2013}$ composed of self-attention with positional encodings and the masked language model (MLM) objective $\unicode{x2013}$ has emerged as a key component of modern large language models (LLMs). Despite its empirical success, few studies have examined its statistical underpinnings: What statistical model is bidirectional attention implicitly fitting? What sets it apart from its non-attention predecessors? We explore these questions in this paper. The key observation is that fitting a single-layer single-head bidirectional attention, upon reparameterization, is equivalent to fitting a continuous bag of words (CBOW) model with mixture-of-experts (MoE) weights. Further, bidirectional attention with multiple heads and multiple layers is equivalent to stacked MoEs and a mixture of MoEs, respectively. This statistical viewpoint reveals the distinct use of MoE in bidirectional attention, which aligns with its practical effectiveness in handling heterogeneous data. It also suggests an immediate extension to categorical tabular data, if we view each word location in a sentence as a tabular feature. Across empirical studies, we find that this extension outperforms existing tabular extensions of transformers in out-of-distribution (OOD) generalization. Finally, this statistical perspective of bidirectional attention enables us to theoretically characterize when linear word analogies are present in its word embeddings. These analyses show that bidirectional attention can require much stronger assumptions to exhibit linear word analogies than its non-attention predecessors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge