Abstracted Gaussian Prototypes for One-Shot Concept Learning

We introduce a cluster-based generative image segmentation framework to encode higher-level representations of visual concepts based on one-shot learning inspired by the Omniglot Challenge. The inferred parameters of each component of a Gaussian Mixture Model (GMM) represent a distinct topological subpart of a visual concept. Sampling new data from these parameters generates augmented subparts to build a more robust prototype for each concept, i.e., the Abstracted Gaussian Prototype (AGP). This framework addresses one-shot classification tasks using a cognitively-inspired similarity metric and addresses one-shot generative tasks through a novel AGP-VAE pipeline employing variational autoencoders (VAEs) to generate new class variants. Results from human judges reveal that the generative pipeline produces novel examples and classes of visual concepts that are broadly indistinguishable from those made by humans. The proposed framework leads to impressive but not state-of-the-art classification accuracy; thus, the contribution is two-fold: 1) the system is uniquely low in theoretical and computational complexity and operates in a completely standalone manner compared while existing approaches draw heavily on pre-training or knowledge engineering; and 2) in contrast with competing neural network models, the AGP approach addresses the importance of breadth of task capability emphasized in the Omniglot challenge (i.e., successful performance on generative tasks). These two points are critical as we advance toward an understanding of how learning/reasoning systems can produce viable, robust, and flexible concepts based on literally nothing more than a single example.

Complexity Measures and Concept Learning

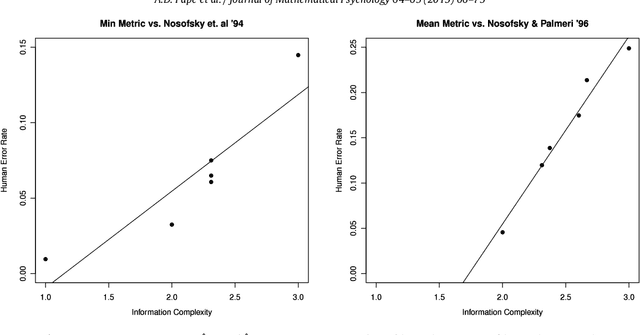
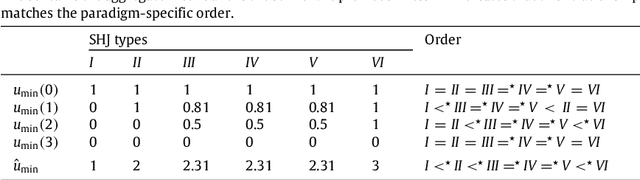
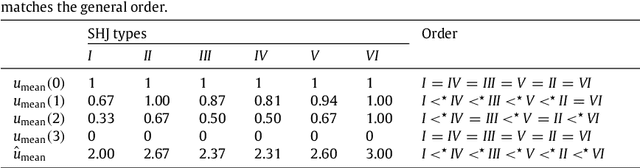
The nature of concept learning is a core question in cognitive science. Theories must account for the relative difficulty of acquiring different concepts by supervised learners. For a canonical set of six category types, two distinct orderings of classification difficulty have been found. One ordering, which we call paradigm-specific, occurs when adult human learners classify objects with easily distinguishable characteristics such as size, shape, and shading. The general order occurs in all other known cases: when adult humans classify objects with characteristics that are not readily distinguished (e.g., brightness, saturation, hue); for children and monkeys; and when categorization difficulty is extrapolated from errors in identification learning. The paradigm-specific order was found to be predictable mathematically by measuring the logical complexity of tasks, i.e., how concisely the solution can be represented by logical rules. However, logical complexity explains only the paradigm-specific order but not the general order. Here we propose a new difficulty measurement, information complexity, that calculates the amount of uncertainty remaining when a subset of the dimensions are specified. This measurement is based on Shannon entropy. We show that, when the metric extracts minimal uncertainties, this new measurement predicts the paradigm-specific order for the canonical six category types, and when the metric extracts average uncertainties, this new measurement predicts the general order. Moreover, for learning category types beyond the canonical six, we find that the minimal-uncertainty formulation correctly predicts the paradigm-specific order as well or better than existing metrics (Boolean complexity and GIST) in most cases.