Kenneth Borup
Distilling from Similar Tasks for Transfer Learning on a Budget
Apr 24, 2023



Abstract:We address the challenge of getting efficient yet accurate recognition systems with limited labels. While recognition models improve with model size and amount of data, many specialized applications of computer vision have severe resource constraints both during training and inference. Transfer learning is an effective solution for training with few labels, however often at the expense of a computationally costly fine-tuning of large base models. We propose to mitigate this unpleasant trade-off between compute and accuracy via semi-supervised cross-domain distillation from a set of diverse source models. Initially, we show how to use task similarity metrics to select a single suitable source model to distill from, and that a good selection process is imperative for good downstream performance of a target model. We dub this approach DistillNearest. Though effective, DistillNearest assumes a single source model matches the target task, which is not always the case. To alleviate this, we propose a weighted multi-source distillation method to distill multiple source models trained on different domains weighted by their relevance for the target task into a single efficient model (named DistillWeighted). Our methods need no access to source data, and merely need features and pseudo-labels of the source models. When the goal is accurate recognition under computational constraints, both DistillNearest and DistillWeighted approaches outperform both transfer learning from strong ImageNet initializations as well as state-of-the-art semi-supervised techniques such as FixMatch. Averaged over 8 diverse target tasks our multi-source method outperforms the baselines by 5.6%-points and 4.5%-points, respectively.
Self-Distillation for Gaussian Process Regression and Classification
Apr 05, 2023Abstract:We propose two approaches to extend the notion of knowledge distillation to Gaussian Process Regression (GPR) and Gaussian Process Classification (GPC); data-centric and distribution-centric. The data-centric approach resembles most current distillation techniques for machine learning, and refits a model on deterministic predictions from the teacher, while the distribution-centric approach, re-uses the full probabilistic posterior for the next iteration. By analyzing the properties of these approaches, we show that the data-centric approach for GPR closely relates to known results for self-distillation of kernel ridge regression and that the distribution-centric approach for GPR corresponds to ordinary GPR with a very particular choice of hyperparameters. Furthermore, we demonstrate that the distribution-centric approach for GPC approximately corresponds to data duplication and a particular scaling of the covariance and that the data-centric approach for GPC requires redefining the model from a Binomial likelihood to a continuous Bernoulli likelihood to be well-specified. To the best of our knowledge, our proposed approaches are the first to formulate knowledge distillation specifically for Gaussian Process models.
Even your Teacher Needs Guidance: Ground-Truth Targets Dampen Regularization Imposed by Self-Distillation
Feb 25, 2021
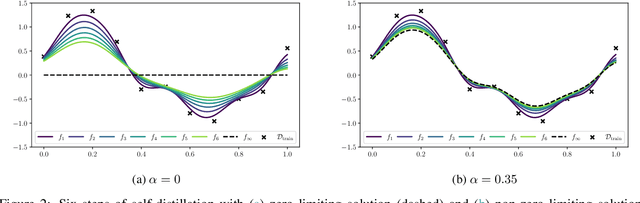
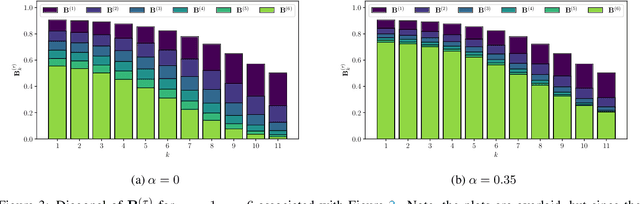
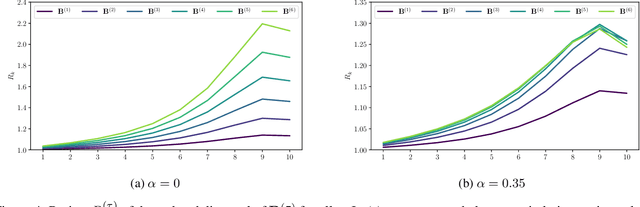
Abstract:Knowledge distillation is classically a procedure where a neural network is trained on the output of another network along with the original targets in order to transfer knowledge between the architectures. The special case of self-distillation, where the network architectures are identical, has been observed to improve generalization accuracy. In this paper, we consider an iterative variant of self-distillation in a kernel regression setting, in which successive steps incorporate both model outputs and the ground-truth targets. This allows us to provide the first theoretical results on the importance of using the weighted ground-truth targets in self-distillation. Our focus is on fitting nonlinear functions to training data with a weighted mean square error objective function suitable for distillation, subject to $\ell_2$ regularization of the model parameters. We show that any such function obtained with self-distillation can be calculated directly as a function of the initial fit, and that infinite distillation steps yields the same optimization problem as the original with amplified regularization. Finally, we examine empirically, both in a regression setting and with ResNet networks, how the choice of weighting parameter influences the generalization performance after self-distillation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge