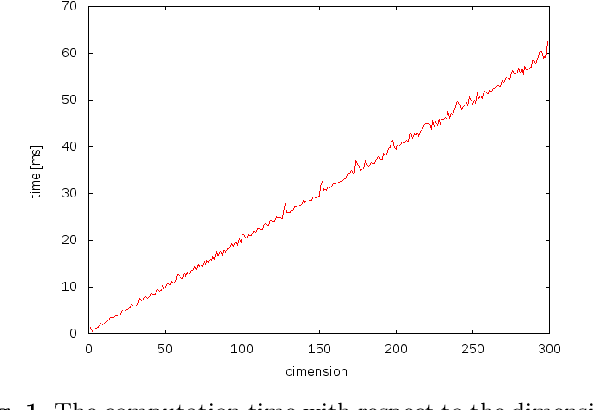
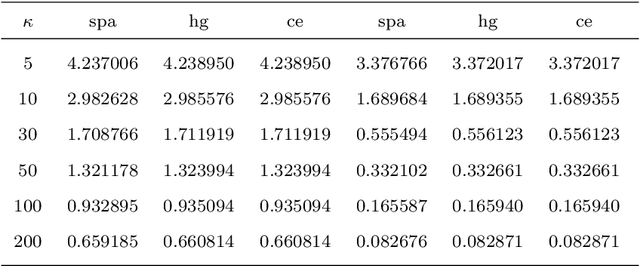
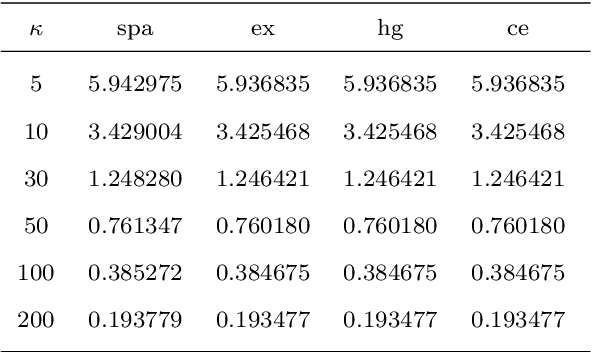
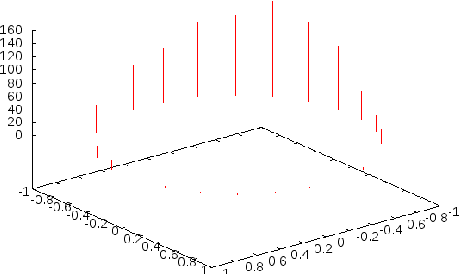
Maximum likelihood estimation of the Fisher-Bingham distribution via efficient calculation of its normalizing constant

This paper proposes an efficient numerical integration formula to compute the normalizing constant of Fisher--Bingham distributions. This formula uses a numerical integration formula with the continuous Euler transform to a Fourier-type integral representation of the normalizing constant. As this method is fast and accurate, it can be applied to the calculation of the normalizing constant of high-dimensional Fisher--Bingham distributions. More precisely, the error decays exponentially with an increase in the integration points, and the computation cost increases linearly with the dimensions. In addition, this formula is useful for calculating the gradient and Hessian matrix of the normalizing constant. Therefore, we apply this formula to efficiently calculate the maximum likelihood estimation (MLE) of high-dimensional data. Finally, we apply the MLE to the hyperspherical variational auto-encoder (S-VAE), a deep-learning-based generative model that restricts the latent space to a unit hypersphere. We use the S-VAE trained with images of handwritten numbers to estimate the distributions of each label. This application is useful for adding new labels to the models.

Enhancing Passive Non-Line-of-Sight Imaging Using Polarization Cues

This paper presents a method of passive non-line-of-sight (NLOS) imaging using polarization cues. A key observation is that the oblique light has a different polarimetric signal. It turns out this effect is due to the polarization axis rotation, a phenomena which can be used to better condition the light transport matrix for non-line-of-sight imaging. Our analysis and results show that the use of a polarizer in front of the camera is not only a separate technique, but it can be seen as an enhancement technique for more advanced forms of passive NLOS imaging. For example, this paper shows that polarization can enhance passive NLOS imaging both with and without occluders. In all tested cases, despite the light attenuation from polarization optics, recovery of the occluded images is improved.