Keli Guo
Optimal prediction for kernel-based semi-functional linear regression
Oct 29, 2021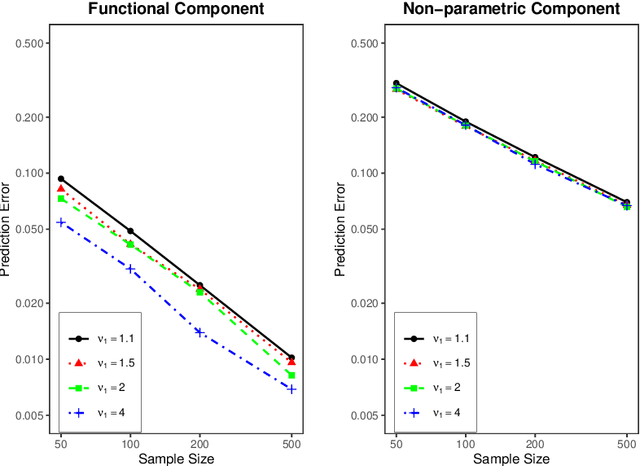
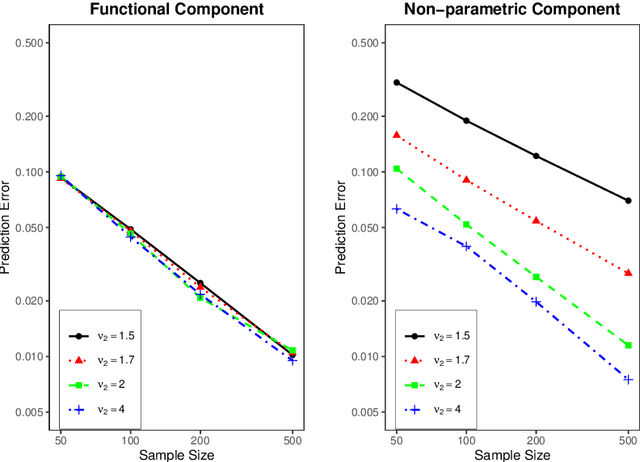
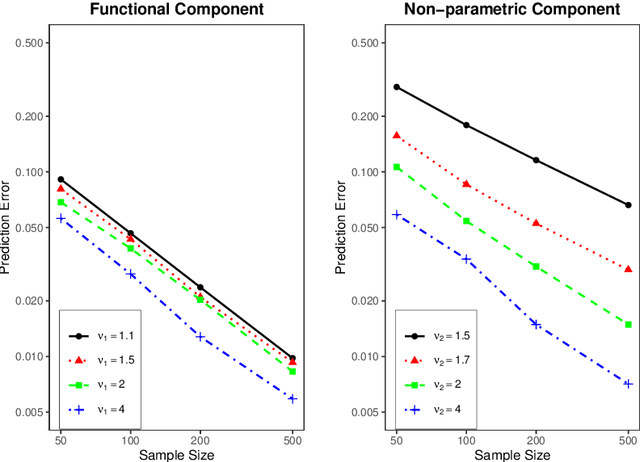
Abstract:In this paper, we establish minimax optimal rates of convergence for prediction in a semi-functional linear model that consists of a functional component and a less smooth nonparametric component. Our results reveal that the smoother functional component can be learned with the minimax rate as if the nonparametric component were known. More specifically, a double-penalized least squares method is adopted to estimate both the functional and nonparametric components within the framework of reproducing kernel Hilbert spaces. By virtue of the representer theorem, an efficient algorithm that requires no iterations is proposed to solve the corresponding optimization problem, where the regularization parameters are selected by the generalized cross validation criterion. Numerical studies are provided to demonstrate the effectiveness of the method and to verify the theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge