Circuit Complexity of Visual Search

We study computational hardness of feature and conjunction search through the lens of circuit complexity. Let $x = (x_1, ... , x_n)$ (resp., $y = (y_1, ... , y_n)$) be Boolean variables each of which takes the value one if and only if a neuron at place $i$ detects a feature (resp., another feature). We then simply formulate the feature and conjunction search as Boolean functions ${\rm FTR}_n(x) = \bigvee_{i=1}^n x_i$ and ${\rm CONJ}_n(x, y) = \bigvee_{i=1}^n x_i \wedge y_i$, respectively. We employ a threshold circuit or a discretized circuit (such as a sigmoid circuit or a ReLU circuit with discretization) as our models of neural networks, and consider the following four computational resources: [i] the number of neurons (size), [ii] the number of levels (depth), [iii] the number of active neurons outputting non-zero values (energy), and [iv] synaptic weight resolution (weight). We first prove that any threshold circuit $C$ of size $s$, depth $d$, energy $e$ and weight $w$ satisfies $\log rk(M_C) \le ed (\log s + \log w + \log n)$, where $rk(M_C)$ is the rank of the communication matrix $M_C$ of a $2n$-variable Boolean function that $C$ computes. Since ${\rm CONJ}_n$ has rank $2^n$, we have $n \le ed (\log s + \log w + \log n)$. Thus, an exponential lower bound on the size of even sublinear-depth threshold circuits exists if the energy and weight are sufficiently small. Since ${\rm FTR}_n$ is computable independently of $n$, our result suggests that computational capacity for the feature and conjunction search are different. We also show that the inequality is tight up to a constant factor if $ed = o(n/ \log n)$. We next show that a similar inequality holds for any discretized circuit. Thus, if we regard the number of gates outputting non-zero values as a measure for sparse activity, our results suggest that larger depth helps neural networks to acquire sparse activity.

A Generalization of Spatial Monte Carlo Integration

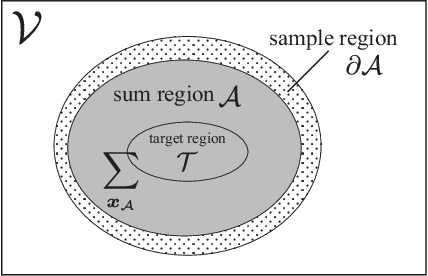
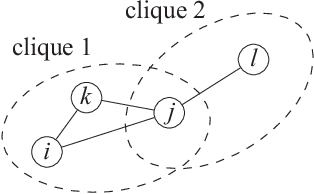
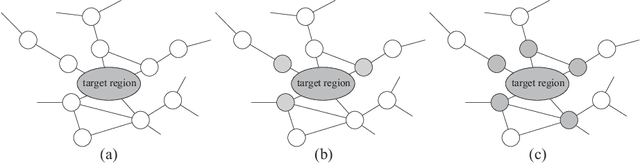
Spatial Monte Carlo integration (SMCI) is an extension of standard Monte Carlo integration and can approximate expectations on Markov random fields with high accuracy. SMCI was applied to pairwise Boltzmann machine (PBM) learning, with superior results to those from some existing methods. The approximation level of SMCI can be changed, and it was proved that a higher-order approximation of SMCI is statistically more accurate than a lower-order approximation. However, SMCI as proposed in the previous studies suffers from a limitation that prevents the application of a higher-order method to dense systems. This study makes two different contributions as follows. A generalization of SMCI (called generalized SMCI (GSMCI)) is proposed, which allows relaxation of the above-mentioned limitation; moreover, a statistical accuracy bound of GSMCI is proved. This is the first contribution of this study. A new PBM learning method based on SMCI is proposed, which is obtained by combining SMCI and the persistent contrastive divergence. The proposed learning method greatly improves the accuracy of learning. This is the second contribution of this study.