Accelerating spherical K-means clustering for large-scale sparse document data

This paper presents an accelerated spherical K-means clustering algorithm for large-scale and high-dimensional sparse document data sets. We design an algorithm working in an architecture-friendly manner (AFM), which is a procedure of suppressing performance-degradation factors such as the numbers of instructions, branch mispredictions, and cache misses in CPUs of a modern computer system. For the AFM operation, we leverage unique universal characteristics (UCs) of a data-object and a cluster's mean set, which are skewed distributions on data relationships such as Zipf's law and a feature-value concentration phenomenon. The UCs indicate that the most part of the number of multiplications for similarity calculations is executed regarding terms with high document frequencies (df) and the most part of a similarity between an object- and a mean-feature vector is obtained by the multiplications regarding a few high mean-feature values. Our proposed algorithm applies an inverted-index data structure to a mean set, extracts the specific region with high-df terms and high mean-feature values in the mean-inverted index by newly introduced two structural parameters, and exploits the index divided into three parts for efficient pruning. The algorithm determines the two structural parameters by minimizing the approximate number of multiplications related to that of instructions, reduces the branch mispredictions by sharing the index structure including the two parameters with all the objects, and suppressing the cache misses by keeping in the caches the frequently used data in the foregoing specific region, resulting in working in the AFM. We experimentally demonstrate that our algorithm efficiently achieves superior speed performance in large-scale documents compared with algorithms using the state-of-the-art techniques.

Structured Inverted-File k-Means Clustering for High-Dimensional Sparse Data

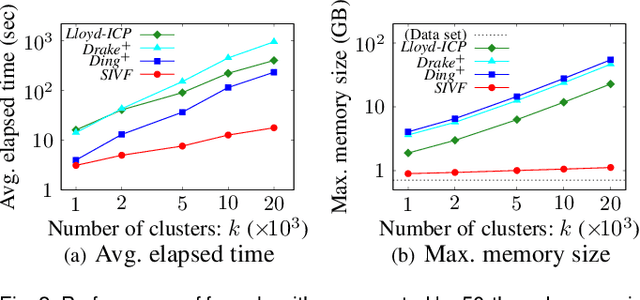
This paper presents an architecture-friendly k-means clustering algorithm called SIVF for a large-scale and high-dimensional sparse data set. Algorithm efficiency on time is often measured by the number of costly operations such as similarity calculations. In practice, however, it depends greatly on how the algorithm adapts to an architecture of the computer system which it is executed on. Our proposed SIVF employs invariant centroid-pair based filter (ICP) to decrease the number of similarity calculations between a data object and centroids of all the clusters. To maximize the ICP performance, SIVF exploits for a centroid set an inverted-file that is structured so as to reduce pipeline hazards. We demonstrate in our experiments on real large-scale document data sets that SIVF operates at higher speed and with lower memory consumption than existing algorithms. Our performance analysis reveals that SIVF achieves the higher speed by suppressing performance degradation factors of the number of cache misses and branch mispredictions rather than less similarity calculations.

Inverted-File k-Means Clustering: Performance Analysis

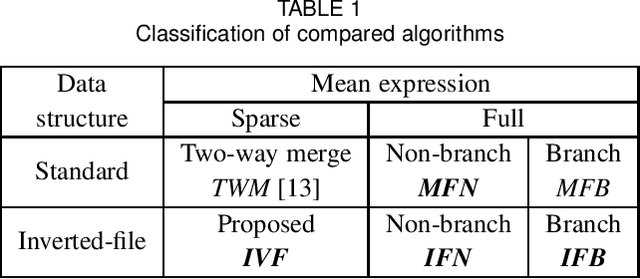
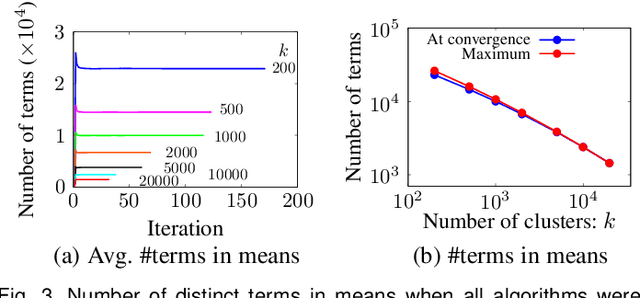
This paper presents an inverted-file k-means clustering algorithm (IVF) suitable for a large-scale sparse data set with potentially numerous classes. Given such a data set, IVF efficiently works at high-speed and with low memory consumption, which keeps the same solution as a standard Lloyd's algorithm. The high performance arises from two distinct data representations. One is a sparse expression for both the object and mean feature vectors. The other is an inverted-file data structure for a set of the mean feature vectors. To confirm the effect of these representations, we design three algorithms using distinct data structures and expressions for comparison. We experimentally demonstrate that IVF achieves better performance than the designed algorithms when they are applied to large-scale real document data sets in a modern computer system equipped with superscalar out-of-order processors and a deep hierarchical memory system. We also introduce a simple yet practical clock-cycle per instruction (CPI) model for speed-performance analysis. Analytical results reveal that IVF suppresses three performance degradation factors: the numbers of cache misses, branch mispredictions, and the completed instructions.