Extension of Convolutional Neural Network along Temporal and Vertical Directions for Precipitation Downscaling

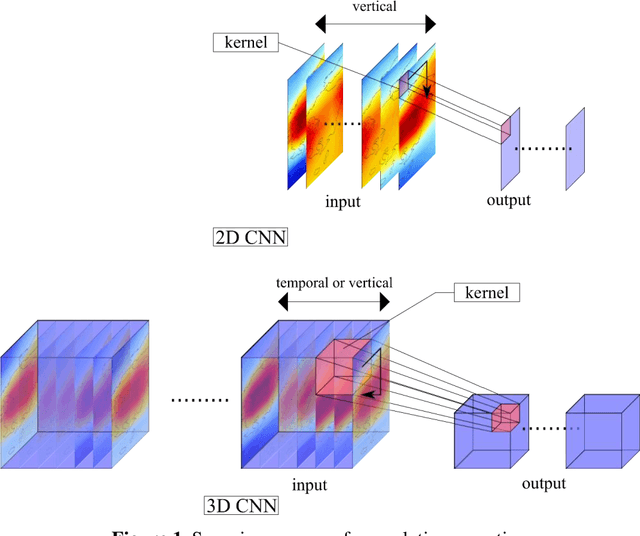
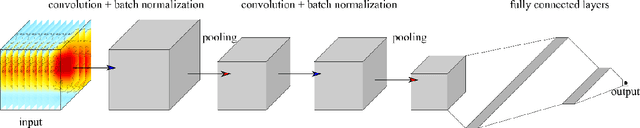
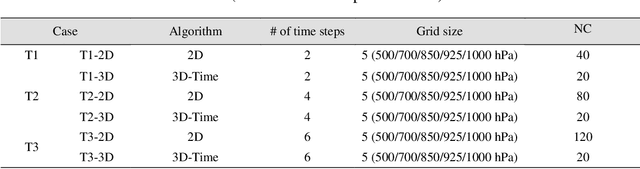
Deep learning has been utilized for the statistical downscaling of climate data. Specifically, a two-dimensional (2D) convolutional neural network (CNN) has been successfully applied to precipitation estimation. This study implements a three-dimensional (3D) CNN to estimate watershed-scale daily precipitation from 3D atmospheric data and compares the results with those for a 2D CNN. The 2D CNN is extended along the time direction (3D-CNN-Time) and the vertical direction (3D-CNN-Vert). The precipitation estimates of these extended CNNs are compared with those of the 2D CNN in terms of the root-mean-square error (RMSE), Nash-Sutcliffe efficiency (NSE), and 99th percentile RMSE. It is found that both 3D-CNN-Time and 3D-CNN-Vert improve the model accuracy for precipitation estimation compared to the 2D CNN. 3D-CNN-Vert provided the best estimates during the training and test periods in terms of RMSE and NSE.

Capabilities of Deep Learning Models on Learning Physical Relationships: Case of Rainfall-Runoff Modeling with LSTM

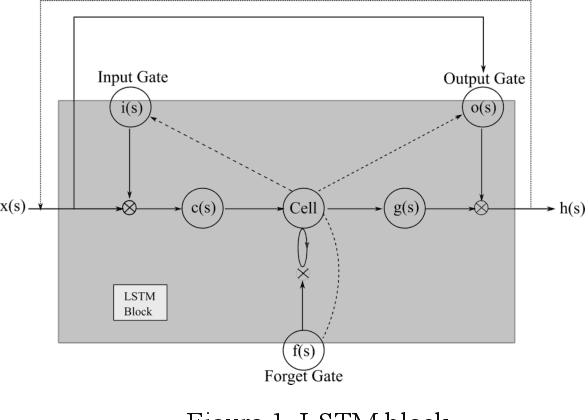
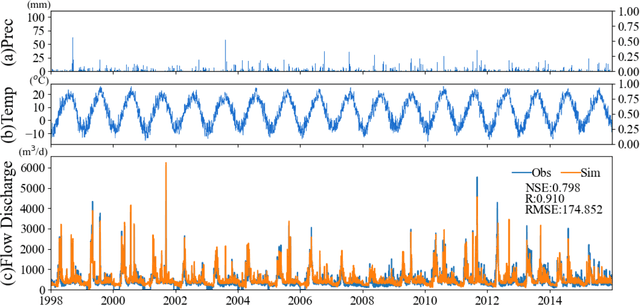
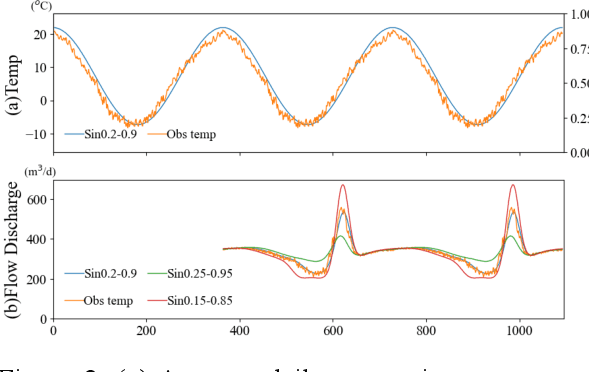
This study investigates the relationships which deep learning methods can identify between the input and output data. As a case study, rainfall-runoff modeling in a snow-dominated watershed by means of a long- and short-term memory (LSTM) network is selected. Daily precipitation and mean air temperature were used as model input to estimate daily flow discharge. After model training and verification, two experimental simulations were conducted with hypothetical inputs instead of observed meteorological data to clarify the response of the trained model to the inputs. The first numerical experiment showed that even without input precipitation, the trained model generated flow discharge, particularly winter low flow and high flow during the snow-melting period. The effects of warmer and colder conditions on the flow discharge were also replicated by the trained model without precipitation. Additionally, the model reflected only 17-39% of the total precipitation mass during the snow accumulation period in the total annual flow discharge, revealing a strong lack of water mass conservation. The results of this study indicated that a deep learning method may not properly learn the explicit physical relationships between input and target variables, although they are still capable of maintaining strong goodness-of-fit results.