Mutual Visibility by Fat Robots with Slim Omnidirectional Camera

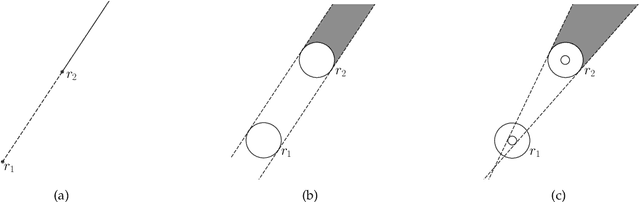
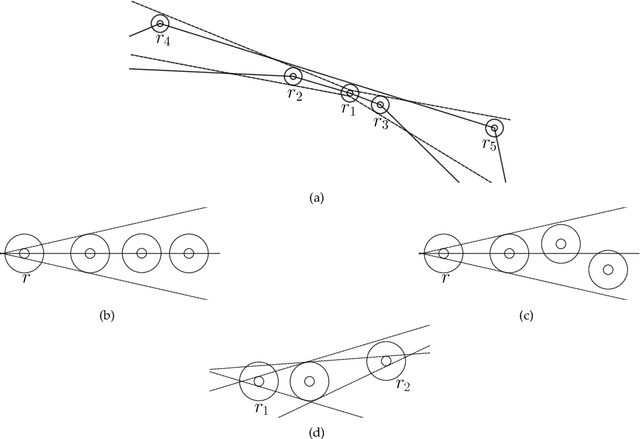
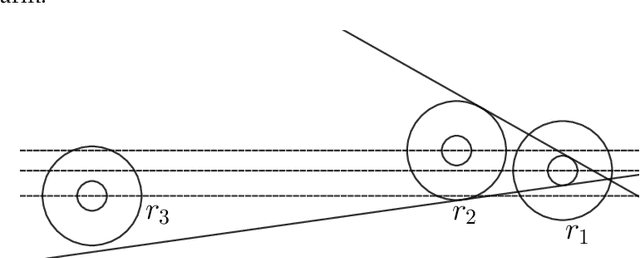
In the existing literature of the Mutual Visibility problem for autonomous robot swarms, the adopted visibility models have some idealistic assumptions that are not consistent with practical sensing device implementations. This paper investigates the problem in the more realistic visibility model called opaque fat robots with slim omnidirectional camera. The robots are modeled as unit disks, each having an omnidirectional camera represented as a disk of smaller size. We assume that the robots have compasses that allow agreement in the direction and orientation of both axes of their local coordinate systems. The robots are equipped with visible lights which serve as a medium of communication and also as a form of memory. We present a distributed algorithm for the Mutual Visibility problem which is provably correct in the semi-synchronous setting. Our algorithm also provides a solution for Leader Election which we use as a subroutine in our main algorithm. Although Leader Election is trivial with two axis agreement in the full visibility model, it is challenging in our case and is of independent interest.

Pattern Formation by Robots with Inaccurate Movements

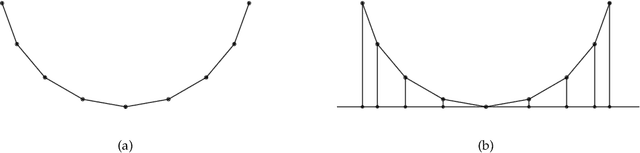
\textsc{Arbitrary Pattern Formation} is a fundamental problem in autonomous mobile robot systems. The problem asks to design a distributed algorithm that moves a team of autonomous, anonymous and identical mobile robots to form any arbitrary pattern $F$ given as input. In this paper, we study the problem for robots whose movements can be inaccurate. Our movement model assumes errors in both direction and extent of the intended movement. Forming the given pattern exactly is not possible in this setting. So we require that the robots must form a configuration which is close to the given pattern $F$. We call this the \textsc{Approximate Arbitrary Pattern Formation} problem. We show that with no agreement in coordinate system, the problem is unsolvable, even by fully synchronous robots, if the initial configuration 1) has rotational symmetry and there is no robot at the center of rotation or 2) has reflectional symmetry and there is no robot on the reflection axis. From all other initial configurations, the problem is solvable by 1) oblivious, silent and semi-synchronous robots and 2) oblivious, asynchronous robots that can communicate using externally visible lights.