Katyanne Farias
Efficient local search limitation strategy for single machine total weighted tardiness scheduling with sequence-dependent setup times
Nov 30, 2015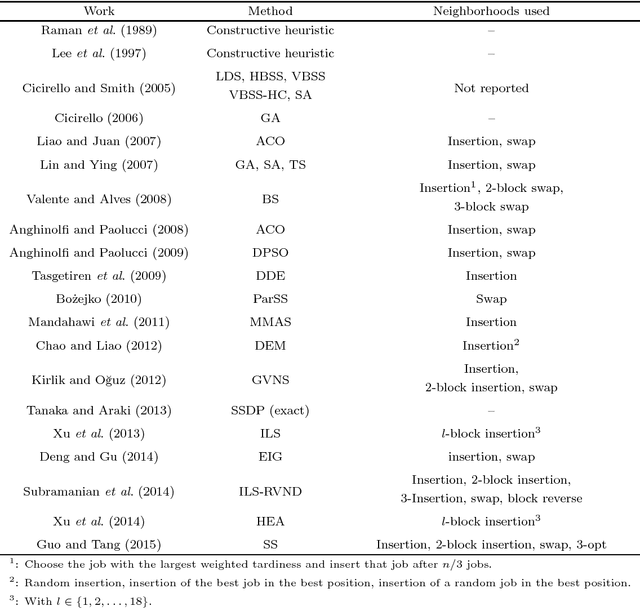

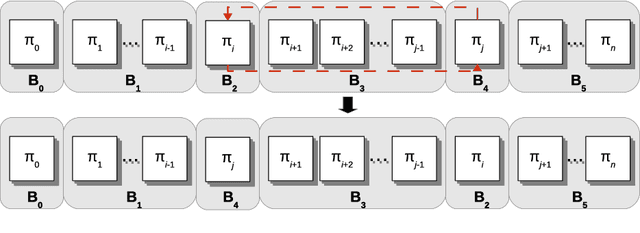
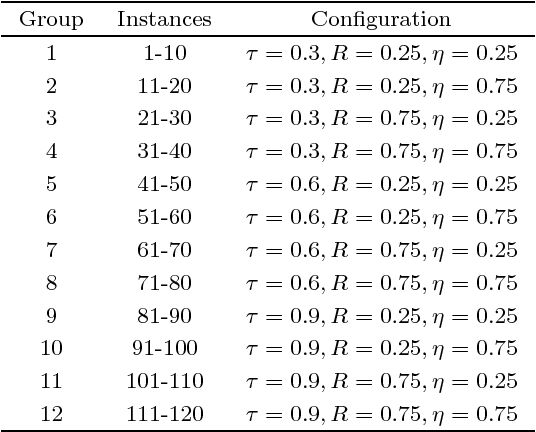
Abstract:This paper concerns the single machine total weighted tardiness scheduling with sequence-dependent setup times, usually referred as $1|s_{ij}|\sum w_jT_j$. In this $\mathcal{NP}$-hard problem, each job has an associated processing time, due date and a weight. For each pair of jobs $i$ and $j$, there may be a setup time before starting to process $j$ in case this job is scheduled immediately after $i$. The objective is to determine a schedule that minimizes the total weighted tardiness, where the tardiness of a job is equal to its completion time minus its due date, in case the job is completely processed only after its due date, and is equal to zero otherwise. Due to its complexity, this problem is most commonly solved by heuristics. The aim of this work is to develop a simple yet effective limitation strategy that speeds up the local search procedure without a significant loss in the solution quality. Such strategy consists of a filtering mechanism that prevents unpromising moves to be evaluated. The proposed strategy has been embedded in a local search based metaheuristic from the literature and tested in classical benchmark instances. Computational experiments revealed that the limitation strategy enabled the metaheuristic to be extremely competitive when compared to other algorithms from the literature, since it allowed the use of a large number of neighborhood structures without a significant increase in the CPU time and, consequently, high quality solutions could be achieved in a matter of seconds. In addition, we analyzed the effectiveness of the proposed strategy in two other well-known metaheuristics. Further experiments were also carried out on benchmark instances of problem $1|s_{ij}|\sum T_j$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge