Kinematic Orienteering Problem With Time-Optimal Trajectories for Multirotor UAVs

In many unmanned aerial vehicle (UAV) applications for surveillance and data collection, it is not possible to reach all requested locations due to the given maximum flight time. Hence, the requested locations must be prioritized and the problem of selecting the most important locations is modeled as an Orienteering Problem (OP). To fully exploit the kinematic properties of the UAV in such scenarios, we combine the OP with the generation of time-optimal trajectories with bounds on velocity and acceleration. We define the resulting problem as the Kinematic Orienteering Problem (KOP) and propose an exact mixed-integer formulation together with a Large Neighborhood Search (LNS) as a heuristic solution method. We demonstrate the effectiveness of our approach based on Orienteering instances from the literature and benchmark against optimal solutions of the Dubins Orienteering Problem (DOP) as the state-of-the-art. Additionally, we show by simulation \color{black} that the resulting solutions can be tracked precisely by a modern MPC-based flight controller. Since we demonstrate that the state-of-the-art in generating time-optimal trajectories in multiple dimensions is not generally correct, we further present an improved analytical method for time-optimal trajectory generation.

Trajectory-based Traveling Salesman Problem for Multirotor UAVs

This paper presents a new method for integrated time-optimal routing and trajectory optimization of multirotor unmanned aerial vehicles (UAVs). Our approach extends the well-known Traveling Salesman Problem by accounting for the limited maneuverability of the UAVs due to their kinematic properties. To this end, we allow each waypoint to be traversed with a discretized velocity as well as a discretized flight direction and compute time-optimal trajectories to determine the travel time costs for each edge. We refer to this novel optimization problem as the Trajectory-based Traveling Salesman Problem (TBTSP). The results show that compared to a state-of-the-art approach for Traveling Salesman Problems with kinematic restrictions of UAVs, we can decrease mission duration by up to 15\%.

Mission planning for emergency rapid mapping with drones

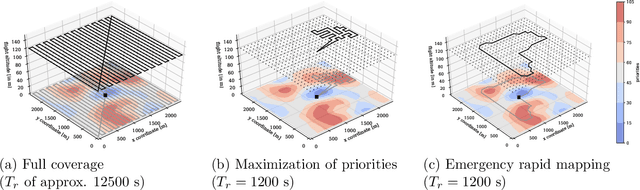
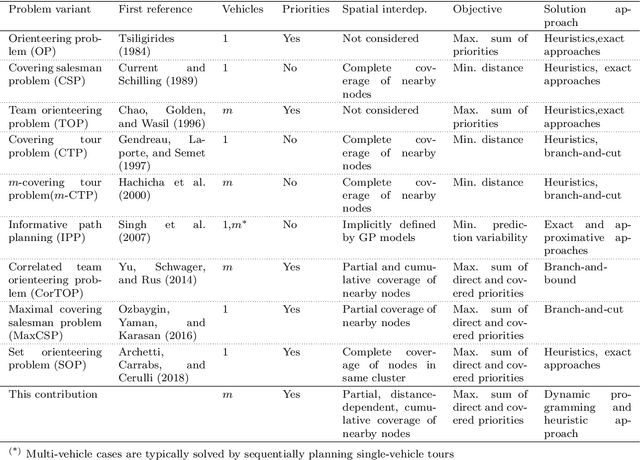
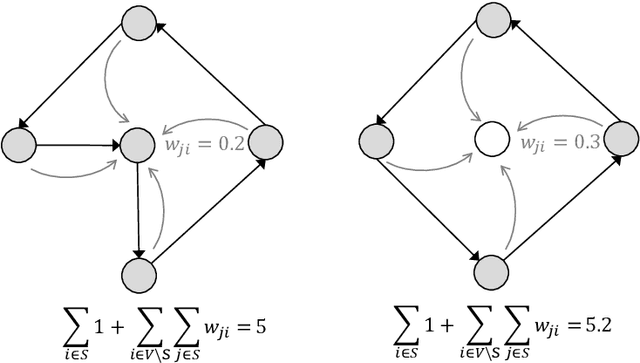
We introduce a mission planning concept for routing unmanned aerial vehicles (UAVs) through a set of sampling locations in the immediate aftermath of an incident such as a fire or chemical accident. Using interpolation methods that account for the spatial interdependencies inherent in the surveyed phenomenon, these samples allow predicting the distribution of hazardous substances across the affected area. We define the generalized correlated team orienteering problem (GCorTOP) for selecting {informative} samples considering spatial correlations between observed and unobserved locations as well as priorities in the surveyed area. To quickly provide high-quality solutions in time-sensitive situations, we propose a two-phase multi-start adaptive large neighborhood search (2MLS). We show the competitiveness of the solution approach using benchmark instances for the team orienteering problem and investigate the performance of the proposed models and solution approach in an extensive study based on newly introduced benchmark instances for the mission planning problem.