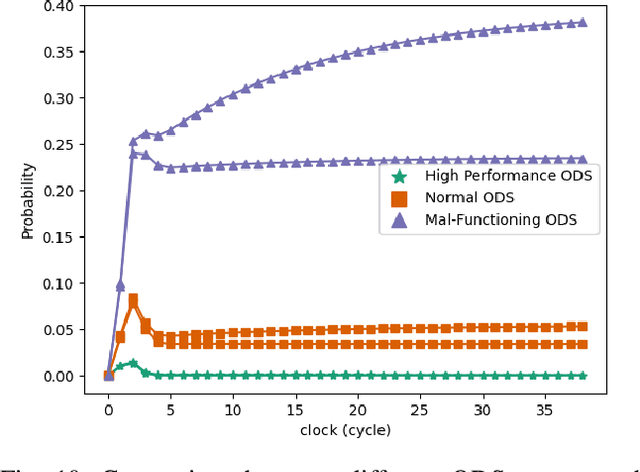
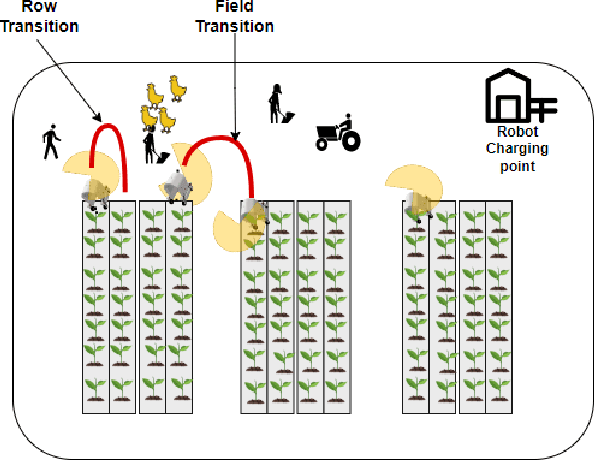
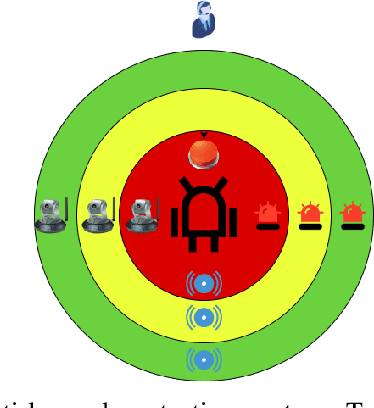
Probabilistic modelling and safety assurance of an agriculture robot providing light-treatment

Continued adoption of agricultural robots postulates the farmer's trust in the reliability, robustness and safety of the new technology. This motivates our work on safety assurance of agricultural robots, particularly their ability to detect, track and avoid obstacles and humans. This paper considers a probabilistic modelling and risk analysis framework for use in the early development phases. Starting off with hazard identification and a risk assessment matrix, the behaviour of the mobile robot platform, sensor and perception system, and any humans present are captured using three state machines. An auto-generated probabilistic model is then solved and analysed using the probabilistic model checker PRISM. The result provides unique insight into fundamental development and engineering aspects by quantifying the effect of the risk mitigation actions and risk reduction associated with distinct design concepts. These include implications of adopting a higher performance and more expensive Object Detection System or opting for a more elaborate warning system to increase human awareness. Although this paper mainly focuses on the initial concept-development phase, the proposed safety assurance framework can also be used during implementation, and subsequent deployment and operation phases.

RoboCertProb: Property Specification for Probabilistic RoboChart Models

RoboChart is a core notation in the RoboStar framework which brings modern modelling and formal verification technologies into software engineering for robotics. It is a timed and probabilistic domain-specific language for robotics and provides a UML-like architectural and state machine modelling. This work presents RoboCertProb for specifying quantitative properties of probabilistic robotic systems modelled in RoboChart. RoboCertProb's semantics is based on PCTL*. To interpret RoboCertProb over RoboChart models, we give a Markov semantics (DTMCs and MDPs) to RoboChart, derived from its existing transformation semantics to the PRISM language. In addition to property specification, RoboCertProb also entitles us to configure loose constants and unspecified functions and operations in RoboChart models. It allows us to set up environmental inputs to verify reactive probabilistic systems not directly supported in probabilistic model checkers like PRISM because they employ a closed-world assumption. We implement RoboCertProb in an accompanying tool of RoboChart, RoboTool, for specifying properties and automatically generating PRISM properties from them to formally verify RoboChart models using PRISM. We have used it to analyse the behaviour of software controllers for two real robots: an industrial painting robot and an agricultural robot for treating plants with UV lights.

Probabilistic relations for modelling epistemic and aleatoric uncertainty: its semantics and automated reasoning with theorem proving

Probabilistic programming is a programming paradigm that combines general computer programming, statistical inference, and formal semantics to help systems to made decisions when facing uncertainty. Probabilistic programs are ubiquitous and believed to have a major impact on machine intelligence. While many probabilistic algorithms have been used in practice in different domains, their automated verification based on formal semantics is still a relatively new research area. In the last two decades, it has been attracting a lot of interest. Many challenges, however, still remain. Our work presented in this paper, probabilistic relations, takes a step into our vision to tackle these challenges. Our work in essence is based on Hehner's predicative probabilistic programming, but there are several obstacles to the wider adoption of his work. Our contributions here include (1) the formalisation of its syntax and semantics by introducing an Iverson bracket notation to separate relations from arithmetic; (2) the formalisation of relations using Unifying Theories of Programming (UTP) and probabilities outside the brackets using summation over the topological space of the real numbers; (3) the constructive semantics for probabilistic loops using the Kleene's fixed point theorem; (4) the enrichment of its semantics from distributions to subdistributions and superdistributions in order to deal with the constructive semantics; (5) the unique fixed point theorem to largely simplify the reasoning about probabilistic loops; and (6) the mechanisation of our theory in Isabelle/UTP, an implementation of UTP in Isabelle/HOL, for automated reasoning using theorem proving. We demonstrate six interesting examples, and among them, one is about robot localisation, two are classification problems in machine learning, and two contain probabilistic loops.