Graph neural networks and non-commuting operators

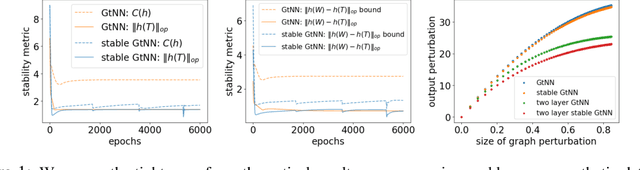
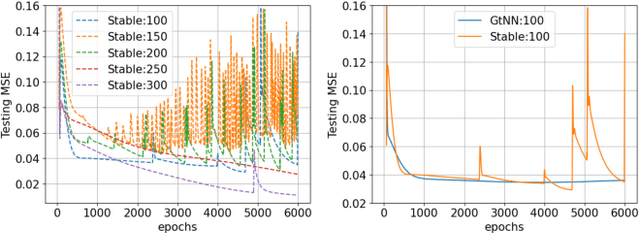
Graph neural networks (GNNs) provide state-of-the-art results in a wide variety of tasks which typically involve predicting features at the vertices of a graph. They are built from layers of graph convolutions which serve as a powerful inductive bias for describing the flow of information among the vertices. Often, more than one data modality is available. This work considers a setting in which several graphs have the same vertex set and a common vertex-level learning task. This generalizes standard GNN models to GNNs with several graph operators that do not commute. We may call this model graph-tuple neural networks (GtNN). In this work, we develop the mathematical theory to address the stability and transferability of GtNNs using properties of non-commuting non-expansive operators. We develop a limit theory of graphon-tuple neural networks and use it to prove a universal transferability theorem that guarantees that all graph-tuple neural networks are transferable on convergent graph-tuple sequences. In particular, there is no non-transferable energy under the convergence we consider here. Our theoretical results extend well-known transferability theorems for GNNs to the case of several simultaneous graphs (GtNNs) and provide a strict improvement on what is currently known even in the GNN case. We illustrate our theoretical results with simple experiments on synthetic and real-world data. To this end, we derive a training procedure that provably enforces the stability of the resulting model.

Metric properties of partial and robust Gromov-Wasserstein distances

The Gromov-Wasserstein (GW) distances define a family of metrics, based on ideas from optimal transport, which enable comparisons between probability measures defined on distinct metric spaces. They are particularly useful in areas such as network analysis and geometry processing, as computation of a GW distance involves solving for registration between the objects which minimizes geometric distortion. Although GW distances have proven useful for various applications in the recent machine learning literature, it has been observed that they are inherently sensitive to outlier noise and cannot accommodate partial matching. This has been addressed by various constructions building on the GW framework; in this article, we focus specifically on a natural relaxation of the GW optimization problem, introduced by Chapel et al., which is aimed at addressing exactly these shortcomings. Our goal is to understand the theoretical properties of this relaxed optimization problem, from the viewpoint of metric geometry. While the relaxed problem fails to induce a metric, we derive precise characterizations of how it fails the axioms of non-degeneracy and triangle inequality. These observations lead us to define a novel family of distances, whose construction is inspired by the Prokhorov and Ky Fan distances, as well as by the recent work of Raghvendra et al.\ on robust versions of classical Wasserstein distance. We show that our new distances define true metrics, that they induce the same topology as the GW distances, and that they enjoy additional robustness to perturbations. These results provide a mathematically rigorous basis for using our robust partial GW distances in applications where outliers and partial matching are concerns.