Kaiming Bi
An Improved Mathematical Model of Sepsis: Modeling, Bifurcation Analysis, and Optimal Control Study for Complex Nonlinear Infectious Disease System
Jan 07, 2022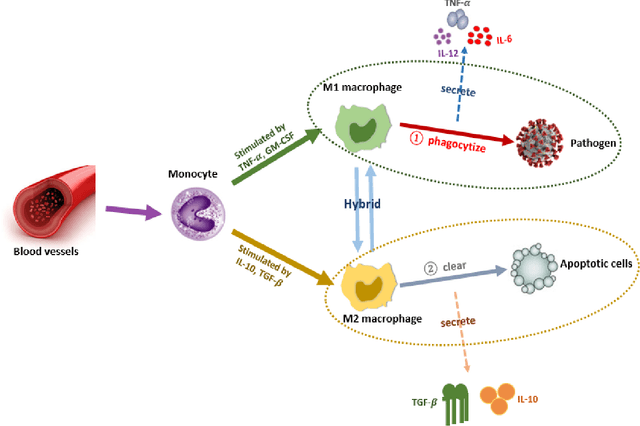

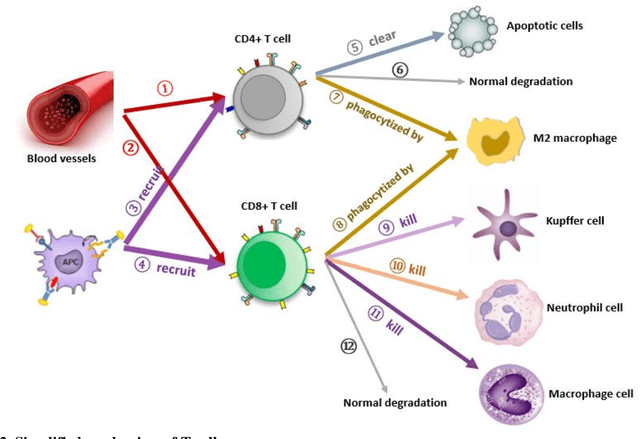

Abstract:Sepsis is a life-threatening medical emergency, which is a major cause of death worldwide and the second highest cause of mortality in the United States. Researching the optimal control treatment or intervention strategy on the comprehensive sepsis system is key in reducing mortality. For this purpose, first, this paper improves a complex nonlinear sepsis model proposed in our previous work. Then, bifurcation analyses are conducted for each sepsis subsystem to study the model behaviors under some system parameters. The bifurcation analysis results also further indicate the necessity of control treatment and intervention therapy. If the sepsis system is without adding any control under some parameter and initial system value settings, the system will perform persistent inflammation outcomes as time goes by. Therefore, we develop our complex improved nonlinear sepsis model into a sepsis optimal control model, and then use some effective biomarkers recommended in existing clinic practices as optimization objective function to measure the development of sepsis. Besides that, a Bayesian optimization algorithm by combining Recurrent neural network (RNN-BO algorithm) is introduced to predict the optimal control strategy for the studied sepsis optimal control system. The difference between the RNN-BO algorithm from other optimization algorithms is that once given any new initial system value setting (initial value is associated with the initial conditions of patients), the RNN-BO algorithm is capable of quickly predicting a corresponding time-series optimal control based on the historical optimal control data for any new sepsis patient. To demonstrate the effectiveness and efficiency of the RNN-BO algorithm on solving the optimal control solution on the complex nonlinear sepsis system, some numerical simulations are implemented by comparing with other optimization algorithms in this paper.
High-dimensional Bayesian Optimization Algorithm with Recurrent Neural Network for Disease Control Models in Time Series
Jan 01, 2022



Abstract:Bayesian Optimization algorithm has become a promising approach for nonlinear global optimization problems and many machine learning applications. Over the past few years, improvements and enhancements have been brought forward and they have shown some promising results in solving the complex dynamic problems, systems of ordinary differential equations where the objective functions are computationally expensive to evaluate. Besides, the straightforward implementation of the Bayesian Optimization algorithm performs well merely for optimization problems with 10-20 dimensions. The study presented in this paper proposes a new high dimensional Bayesian Optimization algorithm combining Recurrent neural networks, which is expected to predict the optimal solution for the global optimization problems with high dimensional or time series decision models. The proposed RNN-BO algorithm can solve the optimal control problems in the lower dimension space and then learn from the historical data using the recurrent neural network to learn the historical optimal solution data and predict the optimal control strategy for any new initial system value setting. In addition, accurately and quickly providing the optimal control strategy is essential to effectively and efficiently control the epidemic spread while minimizing the associated financial costs. Therefore, to verify the effectiveness of the proposed algorithm, computational experiments are carried out on a deterministic SEIR epidemic model and a stochastic SIS optimal control model. Finally, we also discuss the impacts of different numbers of the RNN layers and training epochs on the trade-off between solution quality and related computational efforts.
High dimensional Bayesian Optimization Algorithm for Complex System in Time Series
Aug 04, 2021
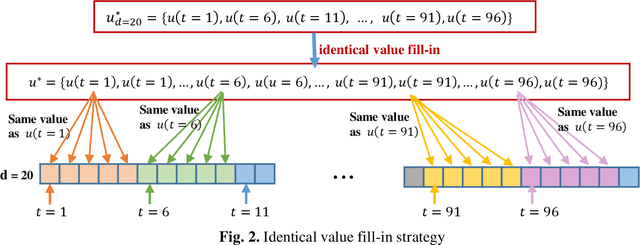

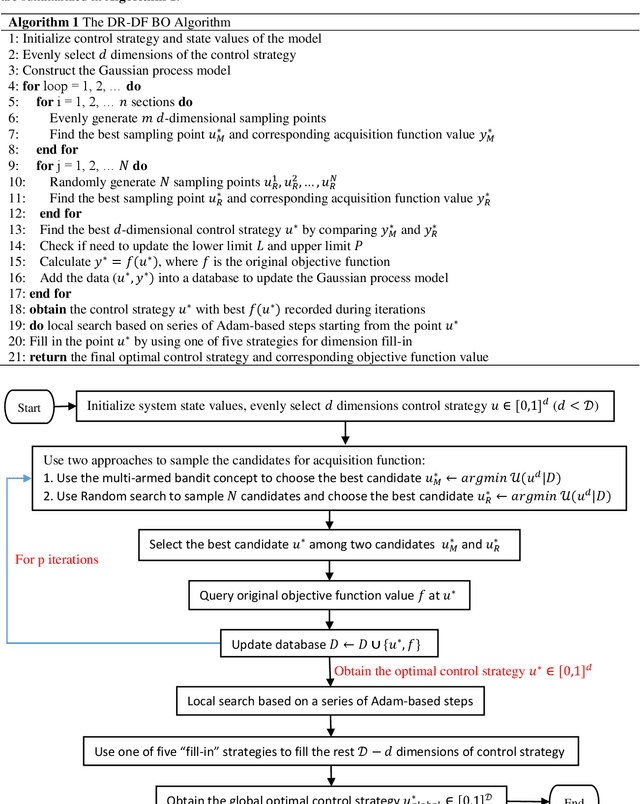
Abstract:At present, high-dimensional global optimization problems with time-series models have received much attention from engineering fields. Since it was proposed, Bayesian optimization has quickly become a popular and promising approach for solving global optimization problems. However, the standard Bayesian optimization algorithm is insufficient to solving the global optimal solution when the model is high-dimensional. Hence, this paper presents a novel high dimensional Bayesian optimization algorithm by considering dimension reduction and different dimension fill-in strategies. Most existing literature about Bayesian optimization algorithms did not discuss the sampling strategies to optimize the acquisition function. This study proposed a new sampling method based on both the multi-armed bandit and random search methods while optimizing the acquisition function. Besides, based on the time-dependent or dimension-dependent characteristics of the model, the proposed algorithm can reduce the dimension evenly. Then, five different dimension fill-in strategies were discussed and compared in this study. Finally, to increase the final accuracy of the optimal solution, the proposed algorithm adds a local search based on a series of Adam-based steps at the final stage. Our computational experiments demonstrated that the proposed Bayesian optimization algorithm could achieve reasonable solutions with excellent performances for high dimensional global optimization problems with a time-series optimal control model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge