Spectral and Temporal Denoising for Differentially Private Optimization

This paper introduces the FFT-Enhanced Kalman Filter (FFTKF), a differentially private optimization method that addresses the challenge of preserving performance in DP-SGD, where added noise typically degrades model utility. FFTKF integrates frequency-domain noise shaping with Kalman filtering to enhance gradient quality while preserving $(\varepsilon, \delta)$-DP guarantees. It employs a high-frequency shaping mask in the Fourier domain to concentrate differential privacy noise in less informative spectral components, preserving low-frequency gradient signals. A scalar-gain Kalman filter with finite-difference Hessian approximation further refines the denoised gradients. With a per-iteration complexity of $\mathcal{O}(d \log d)$, FFTKF demonstrates improved test accuracy over DP-SGD and DiSK across MNIST, CIFAR-10, CIFAR-100, and Tiny-ImageNet datasets using CNNs, Wide ResNets, and Vision Transformers. Theoretical analysis confirms that FFTKF maintains equivalent privacy guarantees while achieving a tighter privacy-utility trade-off through reduced noise and controlled bias.

Sharpness-Aware Minimization with Z-Score Gradient Filtering for Neural Networks

Generalizing well in deep neural networks remains a core challenge, particularly due to their tendency to converge to sharp minima that degrade robustness. Sharpness-Aware Minimization (SAM) mitigates this by seeking flatter minima but perturbs parameters using the full gradient, which can include statistically insignificant directions. We propose ZSharp, a simple yet effective extension to SAM that applies layer-wise Z-score normalization followed by percentile-based filtering to retain only statistically significant gradient components. This selective perturbation aligns updates with curvature-sensitive directions, enhancing generalization without requiring architectural changes. ZSharp introduces only one additional hyperparameter, the percentile threshold, and remains fully compatible with existing SAM variants. Experiments on CIFAR-10, CIFAR-100, and Tiny-ImageNet using ResNet, VGG, and Vision Transformers show that ZSharp consistently outperforms SAM and its variants in test accuracy, particularly on deeper and transformer-based models. These results demonstrate that ZSharp is a principled and lightweight improvement for sharpness-aware optimization.

Mitigating Gradient Overlap in Deep Residual Networks with Gradient Normalization for Improved Non-Convex Optimization

In deep learning, Residual Networks (ResNets) have proven effective in addressing the vanishing gradient problem, allowing for the successful training of very deep networks. However, skip connections in ResNets can lead to gradient overlap, where gradients from both the learned transformation and the skip connection combine, potentially resulting in overestimated gradients. This overestimation can cause inefficiencies in optimization, as some updates may overshoot optimal regions, affecting weight updates. To address this, we examine Z-score Normalization (ZNorm) as a technique to manage gradient overlap. ZNorm adjusts the gradient scale, standardizing gradients across layers and reducing the negative impact of overlapping gradients. Our experiments demonstrate that ZNorm improves training process, especially in non-convex optimization scenarios common in deep learning, where finding optimal solutions is challenging. These findings suggest that ZNorm can affect the gradient flow, enhancing performance in large-scale data processing where accuracy is critical.

ZNorm: Z-Score Gradient Normalization for Accelerating Neural Network Training

The rapid advancements in deep learning necessitate efficient training methods for deep neural networks (DNNs). As models grow in complexity, vanishing and exploding gradients impede convergence and performance. We propose Z-Score Normalization for Gradient Descent (ZNorm), an innovative technique that adjusts only the gradients to enhance training efficiency and improve model performance. ZNorm normalizes the overall gradients, providing consistent gradient scaling across layers, thereby reducing the risks of vanishing and exploding gradients. Our extensive experiments on CIFAR-10 and medical datasets demonstrate that ZNorm not only accelerates convergence but also enhances performance metrics. ZNorm consistently outperforms existing methods, achieving superior results using the same computational settings. In medical imaging applications, ZNorm improves tumor prediction and segmentation performances, underscoring its practical utility. These findings highlight ZNorm's potential as a robust and versatile tool for improving the efficiency and effectiveness of deep neural network training across a wide range of architectures and applications.

Extreme Solar Flare Prediction Using Residual Networks with HMI Magnetograms and Intensitygrams

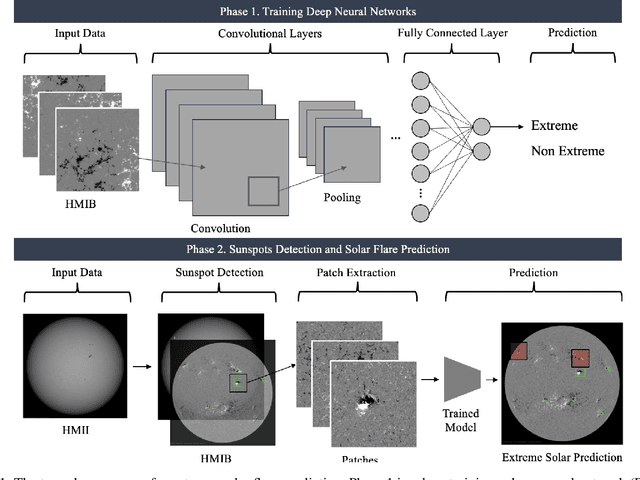
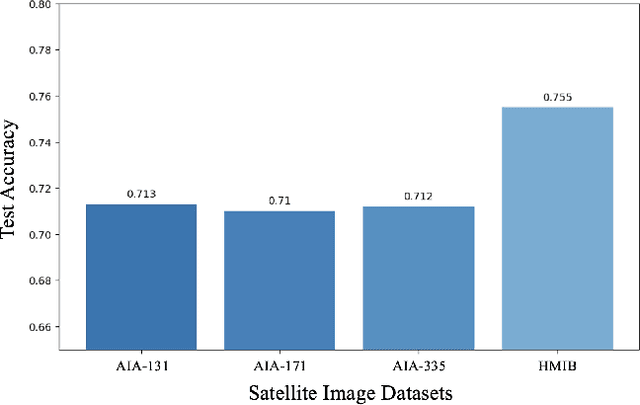
Solar flares, especially C, M, and X class, pose significant risks to satellite operations, communication systems, and power grids. We present a novel approach for predicting extreme solar flares using HMI intensitygrams and magnetograms. By detecting sunspots from intensitygrams and extracting magnetic field patches from magnetograms, we train a Residual Network (ResNet) to classify extreme class flares. Our model demonstrates high accuracy, offering a robust tool for predicting extreme solar flares and improving space weather forecasting. Additionally, we show that HMI magnetograms provide more useful data for deep learning compared to other SDO AIA images by better capturing features critical for predicting flare magnitudes. This study underscores the importance of identifying magnetic fields in solar flare prediction, marking a significant advancement in solar activity prediction with practical implications for mitigating space weather impacts.

Analysis and Predictive Modeling of Solar Coronal Holes Using Computer Vision and LSTM Networks

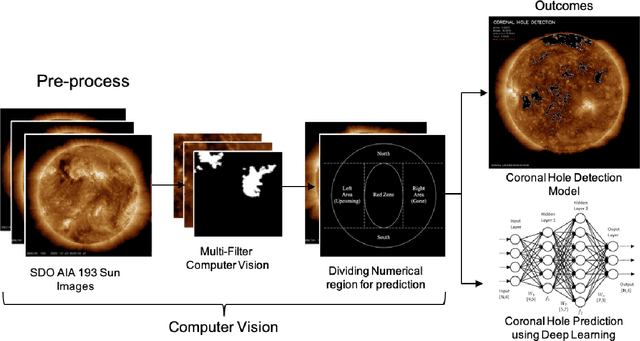
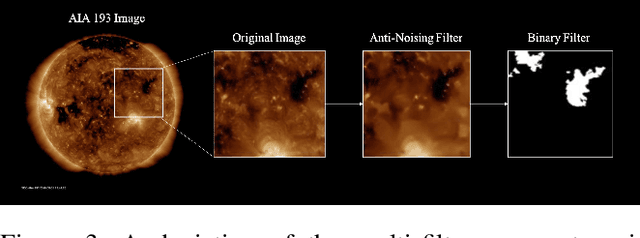
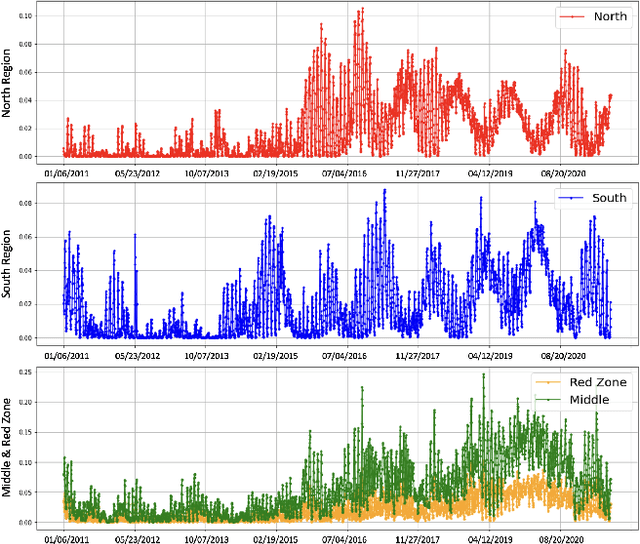
In the era of space exploration, coronal holes on the sun play a significant role due to their impact on satellites and aircraft through their open magnetic fields and increased solar wind emissions. This study employs computer vision techniques to detect coronal hole regions and estimate their sizes using imagery from the Solar Dynamics Observatory (SDO). Additionally, we utilize deep learning methods, specifically Long Short-Term Memory (LSTM) networks, to analyze trends in the area of coronal holes and predict their areas across various solar regions over a span of seven days. By examining time series data, we aim to identify patterns in coronal hole behavior and understand their potential effects on space weather. This research enhances our ability to anticipate and prepare for space weather events that could affect Earth's technological systems.

Robust Neural Pruning with Gradient Sampling Optimization for Residual Neural Networks

In this study, we explore an innovative approach for neural network optimization, focusing on the application of gradient sampling techniques, similar to those in StochGradAdam, during the pruning process. Our primary objective is to maintain high accuracy levels in pruned models, a critical challenge in resource-limited scenarios. Our extensive experiments reveal that models optimized with gradient sampling techniques are more effective at preserving accuracy during pruning compared to those using traditional optimization methods. This finding underscores the significance of gradient sampling in facilitating robust learning and enabling networks to retain crucial information even after substantial reduction in their complexity. We validate our approach across various datasets and neural architectures, demonstrating its broad applicability and effectiveness. The paper also delves into the theoretical aspects, explaining how gradient sampling techniques contribute to the robustness of models during pruning. Our results suggest a promising direction for creating efficient neural networks that do not compromise on accuracy, even in environments with constrained computational resources.

Continuous 16-bit Training: Accelerating 32-bit Pre-Trained Neural Networks

In the field of deep learning, the prevalence of models initially trained with 32-bit precision is a testament to its robustness and accuracy. However, the continuous evolution of these models often demands further training, which can be resource-intensive. This study introduces a novel approach where we continue the training of these pre-existing 32-bit models using 16-bit precision. This technique not only caters to the need for efficiency in computational resources but also significantly improves the speed of additional training phases. By adopting 16-bit precision for ongoing training, we are able to substantially decrease memory requirements and computational burden, thereby accelerating the training process in a resource-limited setting. Our experiments show that this method maintains the high standards of accuracy set by the original 32-bit training while providing a much-needed boost in training speed. This approach is especially pertinent in today's context, where most models are initially trained in 32-bit and require periodic updates and refinements. The findings from our research suggest that this strategy of 16-bit continuation training can be a key solution for sustainable and efficient deep learning, offering a practical way to enhance pre-trained models rapidly and in a resource-conscious manner.

StochGradAdam: Accelerating Neural Networks Training with Stochastic Gradient Sampling

In the rapidly advancing domain of deep learning optimization, this paper unveils the StochGradAdam optimizer, a novel adaptation of the well-regarded Adam algorithm. Central to StochGradAdam is its gradient sampling technique. This method not only ensures stable convergence but also leverages the advantages of selective gradient consideration, fostering robust training by potentially mitigating the effects of noisy or outlier data and enhancing the exploration of the loss landscape for more dependable convergence. In both image classification and segmentation tasks, StochGradAdam has demonstrated superior performance compared to the traditional Adam optimizer. By judiciously sampling a subset of gradients at each iteration, the optimizer is optimized for managing intricate models. The paper provides a comprehensive exploration of StochGradAdam's methodology, from its mathematical foundations to bias correction strategies, heralding a promising advancement in deep learning training techniques.

Linear Oscillation: The Aesthetics of Confusion for Vision Transformer

Activation functions are the linchpins of deep learning, profoundly influencing both the representational capacity and training dynamics of neural networks. They shape not only the nature of representations but also optimize convergence rates and enhance generalization potential. Appreciating this critical role, we present the Linear Oscillation (LoC) activation function, defined as $f(x) = x \times \sin(\alpha x + \beta)$. Distinct from conventional activation functions which primarily introduce non-linearity, LoC seamlessly blends linear trajectories with oscillatory deviations. The nomenclature ``Linear Oscillation'' is a nod to its unique attribute of infusing linear activations with harmonious oscillations, capturing the essence of the 'Importance of Confusion'. This concept of ``controlled confusion'' within network activations is posited to foster more robust learning, particularly in contexts that necessitate discerning subtle patterns. Our empirical studies reveal that, when integrated into diverse neural architectures, the LoC activation function consistently outperforms established counterparts like ReLU and Sigmoid. The stellar performance exhibited by the avant-garde Vision Transformer model using LoC further validates its efficacy. This study illuminates the remarkable benefits of the LoC over other prominent activation functions. It champions the notion that intermittently introducing deliberate complexity or ``confusion'' during training can spur more profound and nuanced learning. This accentuates the pivotal role of judiciously selected activation functions in shaping the future of neural network training.