Efficient Denoising using Score Embedding in Score-based Diffusion Models

It is well known that training a denoising score-based diffusion models requires tens of thousands of epochs and a substantial number of image data to train the model. In this paper, we propose to increase the efficiency in training score-based diffusion models. Our method allows us to decrease the number of epochs needed to train the diffusion model. We accomplish this by solving the log-density Fokker-Planck (FP) Equation numerically to compute the score \textit{before} training. The pre-computed score is embedded into the image to encourage faster training under slice Wasserstein distance. Consequently, it also allows us to decrease the number of images we need to train the neural network to learn an accurate score. We demonstrate through our numerical experiments the improved performance of our proposed method compared to standard score-based diffusion models. Our proposed method achieves a similar quality to the standard method meaningfully faster.

Deep Neural Network Framework Based on Backward Stochastic Differential Equations for Pricing and Hedging American Options in High Dimensions

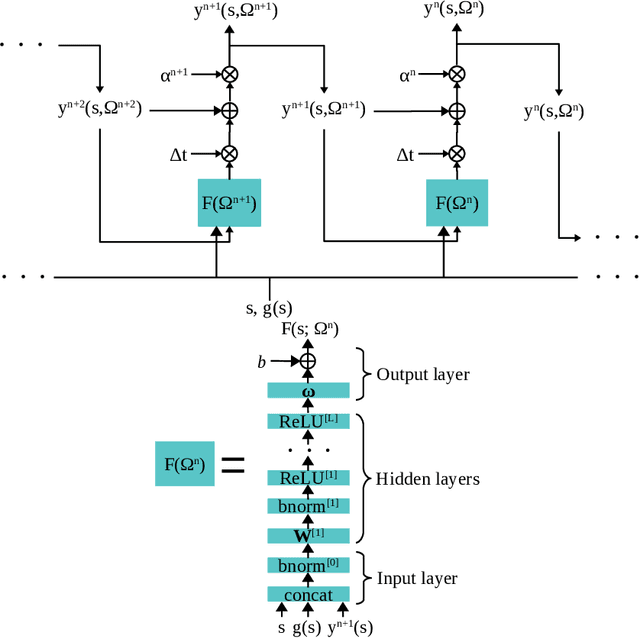
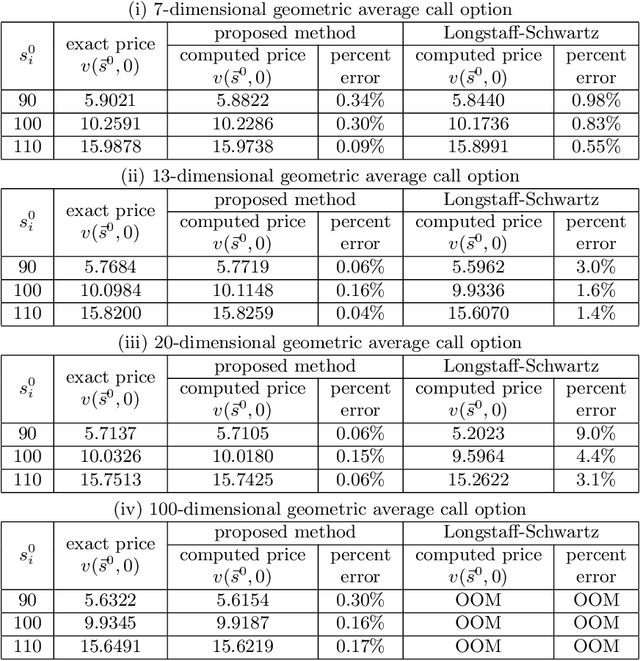
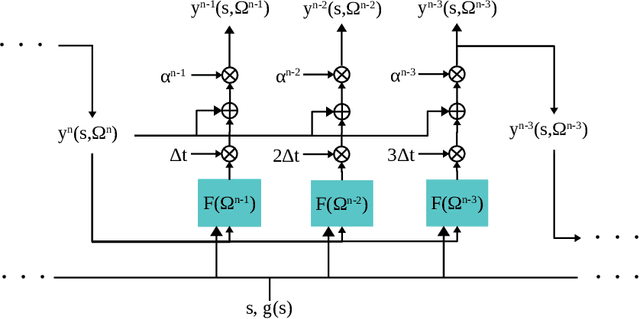
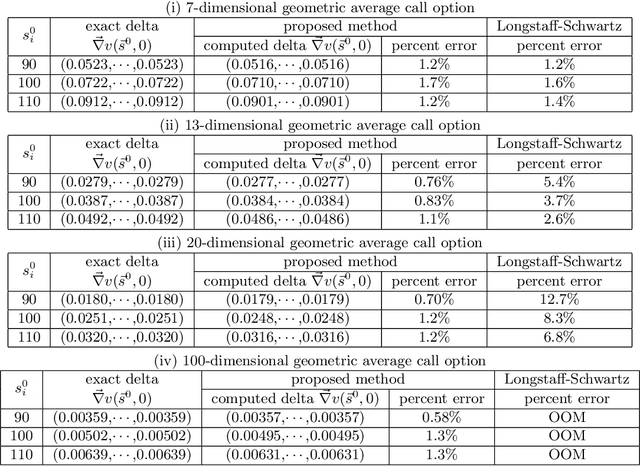
We propose a deep neural network framework for computing prices and deltas of American options in high dimensions. The architecture of the framework is a sequence of neural networks, where each network learns the difference of the price functions between adjacent timesteps. We introduce the least squares residual of the associated backward stochastic differential equation as the loss function. Our proposed framework yields prices and deltas on the entire spacetime, not only at a given point. The computational cost of the proposed approach is quadratic in dimension, which addresses the curse of dimensionality issue that state-of-the-art approaches suffer. Our numerical simulations demonstrate these contributions, and show that the proposed neural network framework outperforms state-of-the-art approaches in high dimensions.