Rethinking generalization of classifiers in separable classes scenarios and over-parameterized regimes

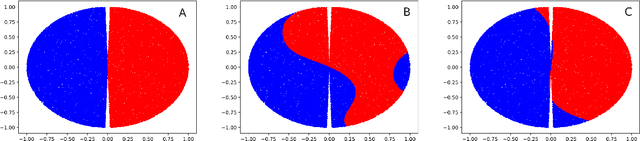
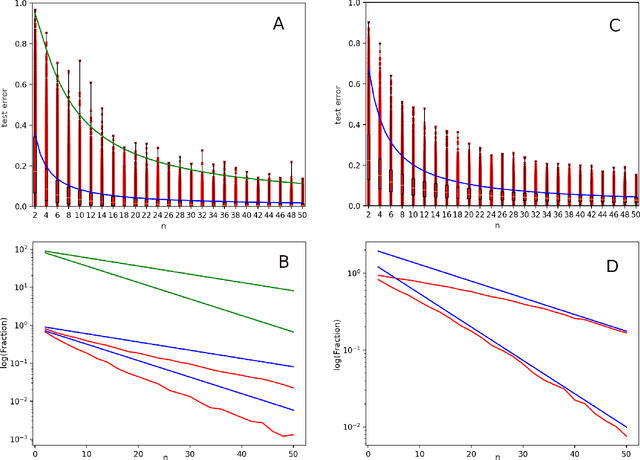
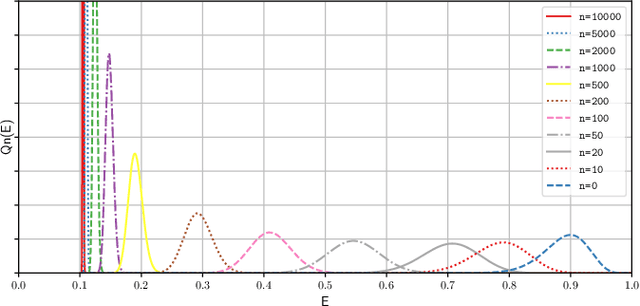
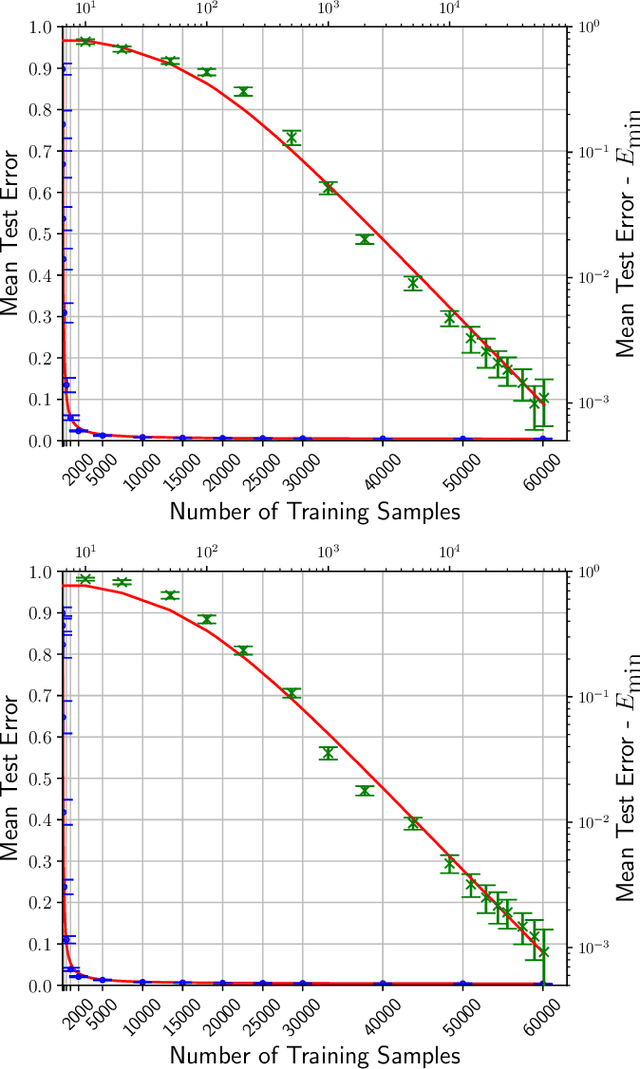
We investigate the learning dynamics of classifiers in scenarios where classes are separable or classifiers are over-parameterized. In both cases, Empirical Risk Minimization (ERM) results in zero training error. However, there are many global minima with a training error of zero, some of which generalize well and some of which do not. We show that in separable classes scenarios the proportion of "bad" global minima diminishes exponentially with the number of training data n. Our analysis provides bounds and learning curves dependent solely on the density distribution of the true error for the given classifier function set, irrespective of the set's size or complexity (e.g., number of parameters). This observation may shed light on the unexpectedly good generalization of over-parameterized Neural Networks. For the over-parameterized scenario, we propose a model for the density distribution of the true error, yielding learning curves that align with experiments on MNIST and CIFAR-10.

Highly over-parameterized classifiers generalize since bad solutions are rare

We study the generalization of over-parameterized classifiers where Empirical Risk Minimization (ERM) for learning leads to zero training error. In these over-parameterized settings there are many global minima with zero training error, some of which generalize better than others. We show that under certain conditions the fraction of "bad" global minima with a true error larger than {\epsilon} decays to zero exponentially fast with the number of training data n. The bound depends on the distribution of the true error over the set of classifier functions used for the given classification problem, and does not necessarily depend on the size or complexity (e.g. the number of parameters) of the classifier function set. This might explain the unexpectedly good generalization even of highly over-parameterized Neural Networks. We support our mathematical framework with experiments on a synthetic data set and a subset of MNIST.