Rethinking generalization of classifiers in separable classes scenarios and over-parameterized regimes
Paper and Code
Oct 22, 2024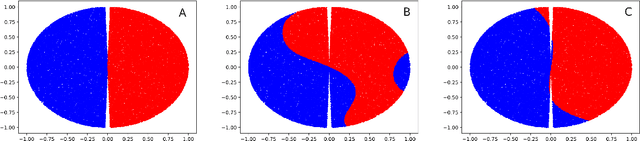
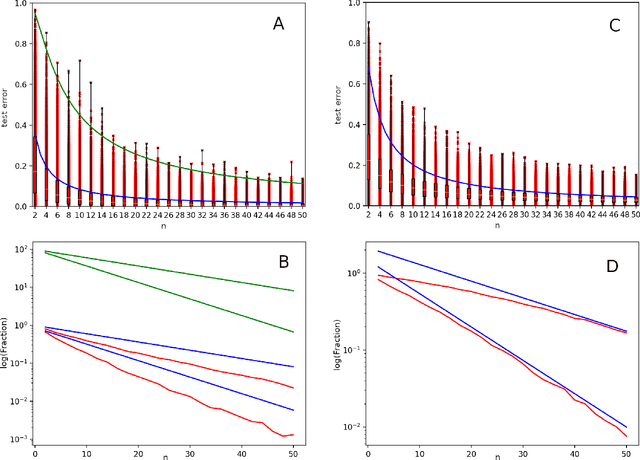
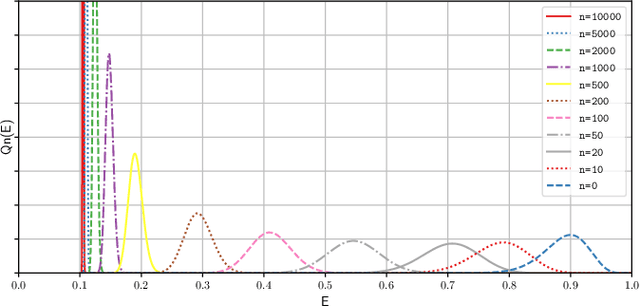
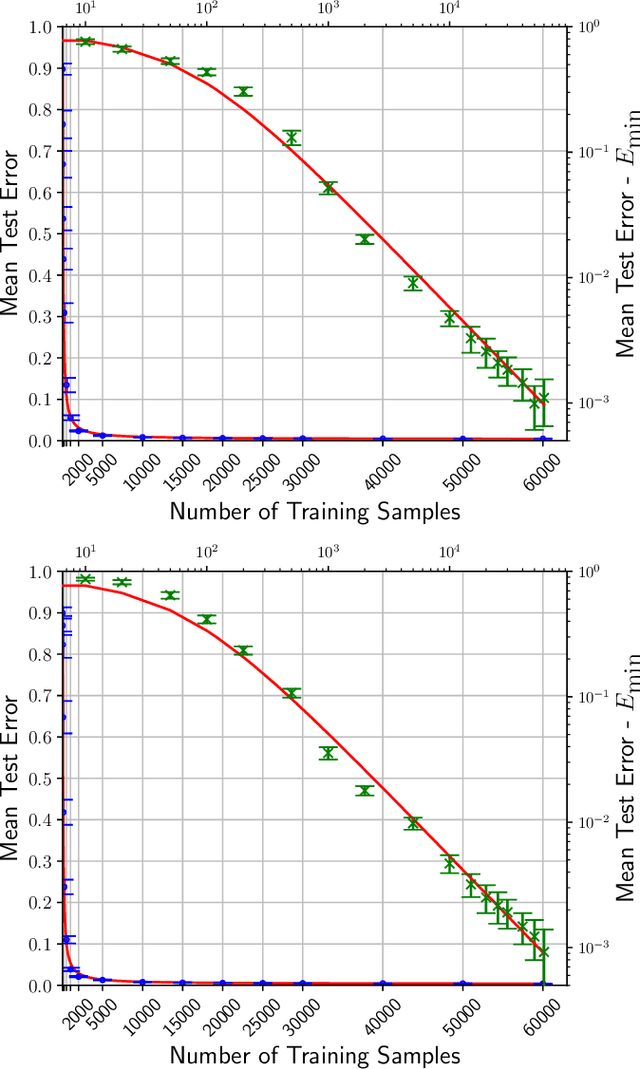
We investigate the learning dynamics of classifiers in scenarios where classes are separable or classifiers are over-parameterized. In both cases, Empirical Risk Minimization (ERM) results in zero training error. However, there are many global minima with a training error of zero, some of which generalize well and some of which do not. We show that in separable classes scenarios the proportion of "bad" global minima diminishes exponentially with the number of training data n. Our analysis provides bounds and learning curves dependent solely on the density distribution of the true error for the given classifier function set, irrespective of the set's size or complexity (e.g., number of parameters). This observation may shed light on the unexpectedly good generalization of over-parameterized Neural Networks. For the over-parameterized scenario, we propose a model for the density distribution of the true error, yielding learning curves that align with experiments on MNIST and CIFAR-10.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge