On the Identification and Optimization of Nonsmooth Superposition Operators in Semilinear Elliptic PDEs

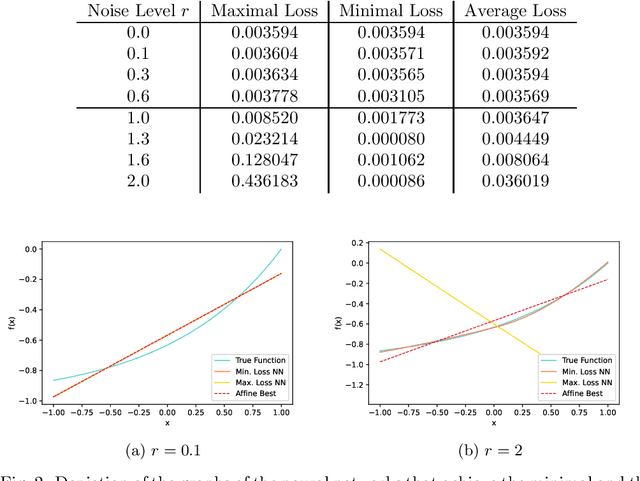
We study an infinite-dimensional optimization problem that aims to identify the Nemytskii operator in the nonlinear part of a prototypical semilinear elliptic partial differential equation (PDE) which minimizes the distance between the PDE-solution and a given desired state. In contrast to previous works, we consider this identification problem in a low-regularity regime in which the function inducing the Nemytskii operator is a-priori only known to be an element of $H^1_{loc}(\mathbb{R})$. This makes the studied problem class a suitable point of departure for the rigorous analysis of training problems for learning-informed PDEs in which an unknown superposition operator is approximated by means of a neural network with nonsmooth activation functions (ReLU, leaky-ReLU, etc.). We establish that, despite the low regularity of the controls, it is possible to derive a classical stationarity system for local minimizers and to solve the considered problem by means of a gradient projection method. The convergence of the resulting algorithm is proven in the function space setting. It is also shown that the established first-order necessary optimality conditions imply that locally optimal superposition operators share various characteristic properties with commonly used activation functions: They are always sigmoidal, continuously differentiable away from the origin, and typically possess a distinct kink at zero. The paper concludes with numerical experiments which confirm the theoretical findings.

On the Omnipresence of Spurious Local Minima in Certain Neural Network Training Problems

We study the loss landscape of training problems for deep artificial neural networks with a one-dimensional real output whose activation functions contain an affine segment and whose hidden layers have width at least two. It is shown that such problems possess a continuum of spurious (i.e., not globally optimal) local minima for all target functions that are not affine. In contrast to previous works, our analysis covers all sampling and parameterization regimes, general differentiable loss functions, arbitrary continuous nonpolynomial activation functions, and both the finite- and infinite-dimensional setting. It is further shown that the appearance of the spurious local minima in the considered training problems is a direct consequence of the universal approximation theorem and that the underlying mechanisms also cause, e.g., Lp-best approximation problems to be ill-posed in the sense of Hadamard for all networks that do not have a dense image. The latter result also holds without the assumption of local affine linearity and without any conditions on the hidden layers. The paper concludes with a numerical experiment which demonstrates that spurious local minima can indeed affect the convergence behavior of gradient-based solution algorithms in practice.