Non-intrusive data-driven model order reduction for circuits based on Hammerstein architectures

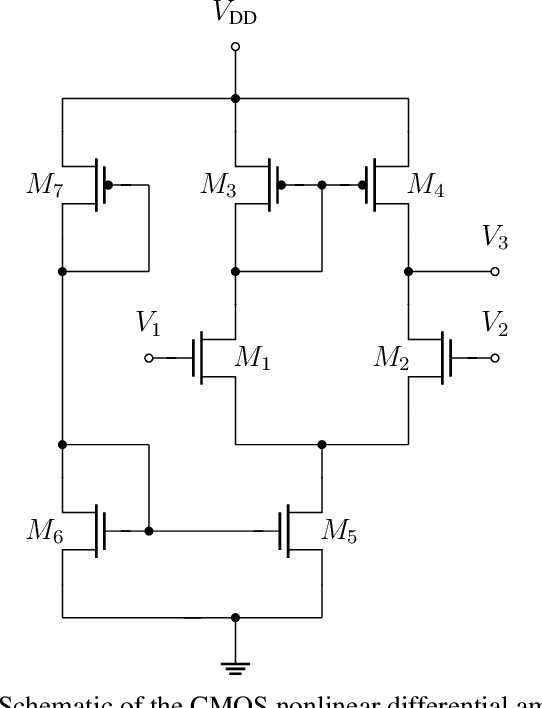
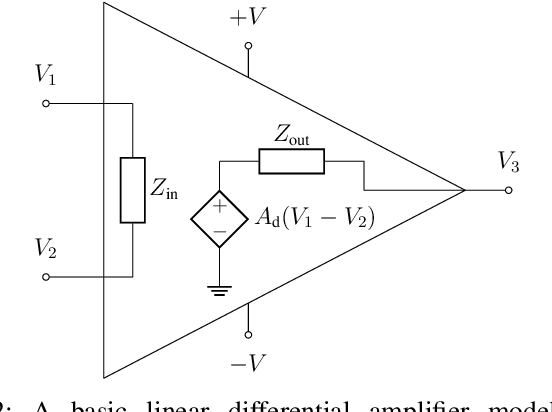
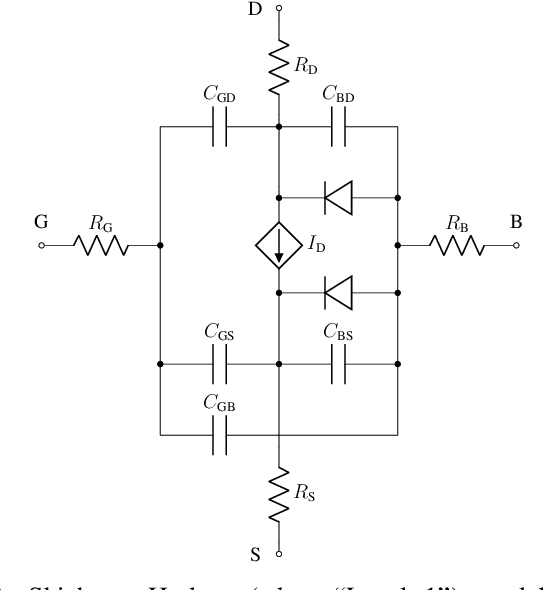
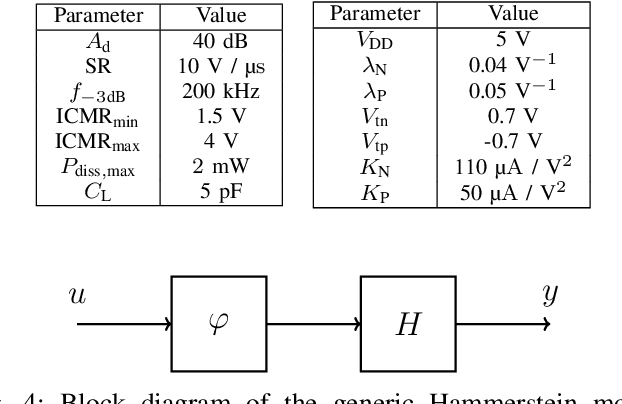
We demonstrate that data-driven system identification techniques can provide a basis for effective, non-intrusive model order reduction (MOR) for common circuits that are key building blocks in microelectronics. Our approach is motivated by the practical operation of these circuits and utilizes a canonical Hammerstein architecture. To demonstrate the approach we develop a parsimonious Hammerstein model for a non-linear CMOS differential amplifier. We train this model on a combination of direct current (DC) and transient Spice (Xyce) circuit simulation data using a novel sequential strategy to identify the static nonlinear and linear dynamical parts of the model. Simulation results show that the Hammerstein model is an effective surrogate for the differential amplifier circuit that accurately and efficiently reproduces its behavior over a wide range of operating points and input frequencies.

Rademacher Complexity of Neural ODEs via Chen-Fliess Series

We show how continuous-depth neural ODE models can be framed as single-layer, infinite-width nets using the Chen--Fliess series expansion for nonlinear ODEs. In this net, the output "weights" are taken from the signature of the control input -- a tool used to represent infinite-dimensional paths as a sequence of tensors -- which comprises iterated integrals of the control input over a simplex. The "features" are taken to be iterated Lie derivatives of the output function with respect to the vector fields in the controlled ODE model. The main result of this work applies this framework to derive compact expressions for the Rademacher complexity of ODE models that map an initial condition to a scalar output at some terminal time. The result leverages the straightforward analysis afforded by single-layer architectures. We conclude with some examples instantiating the bound for some specific systems and discuss potential follow-up work.

Fitting an immersed submanifold to data via Sussmann's orbit theorem

This paper describes an approach for fitting an immersed submanifold of a finite-dimensional Euclidean space to random samples. The reconstruction mapping from the ambient space to the desired submanifold is implemented as a composition of an encoder that maps each point to a tuple of (positive or negative) times and a decoder given by a composition of flows along finitely many vector fields starting from a fixed initial point. The encoder supplies the times for the flows. The encoder-decoder map is obtained by empirical risk minimization, and a high-probability bound is given on the excess risk relative to the minimum expected reconstruction error over a given class of encoder-decoder maps. The proposed approach makes fundamental use of Sussmann's orbit theorem, which guarantees that the image of the reconstruction map is indeed contained in an immersed submanifold.

Learning Recurrent Neural Net Models of Nonlinear Systems

We consider the following learning problem: Given sample pairs of input and output signals generated by an unknown nonlinear system (which is not assumed to be causal or time-invariant), we wish to find a continuous-time recurrent neural net with hyperbolic tangent activation function that approximately reproduces the underlying i/o behavior with high confidence. Leveraging earlier work concerned with matching output derivatives up to a given finite order, we reformulate the learning problem in familiar system-theoretic language and derive quantitative guarantees on the sup-norm risk of the learned model in terms of the number of neurons, the sample size, the number of derivatives being matched, and the regularity properties of the inputs, the outputs, and the unknown i/o map.

Learning Compact Physics-Aware Delayed Photocurrent Models Using Dynamic Mode Decomposition

Radiation-induced photocurrent in semiconductor devices can be simulated using complex physics-based models, which are accurate, but computationally expensive. This presents a challenge for implementing device characteristics in high-level circuit simulations where it is computationally infeasible to evaluate detailed models for multiple individual circuit elements. In this work we demonstrate a procedure for learning compact delayed photocurrent models that are efficient enough to implement in large-scale circuit simulations, but remain faithful to the underlying physics. Our approach utilizes Dynamic Mode Decomposition (DMD), a system identification technique for learning reduced order discrete-time dynamical systems from time series data based on singular value decomposition. To obtain physics-aware device models, we simulate the excess carrier density induced by radiation pulses by solving numerically the Ambipolar Diffusion Equation, then use the simulated internal state as training data for the DMD algorithm. Our results show that the significantly reduced order delayed photocurrent models obtained via this method accurately approximate the dynamics of the internal excess carrier density -- which can be used to calculate the induced current at the device boundaries -- while remaining compact enough to incorporate into larger circuit simulations.

Universal Approximation of Input-Output Maps by Temporal Convolutional Nets

There has been a recent shift in sequence-to-sequence modeling from recurrent network architectures to convolutional network architectures due to computational advantages in training and operation while still achieving competitive performance. For systems having limited long-term temporal dependencies, the approximation capability of recurrent networks is essentially equivalent to that of temporal convolutional nets (TCNs). We prove that TCNs can approximate a large class of input-output maps having approximately finite memory to arbitrary error tolerance. Furthermore, we derive quantitative approximation rates for deep ReLU TCNs in terms of the width and depth of the network and modulus of continuity of the original input-output map, and apply these results to input-output maps of systems that admit finite-dimensional state-space realizations (i.e., recurrent models).