A Sparse Coding Interpretation of Neural Networks and Theoretical Implications

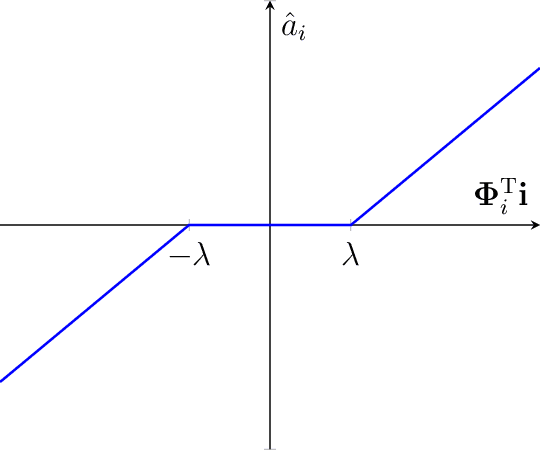
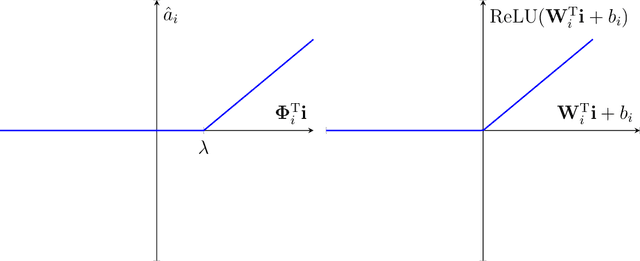
Neural networks, specifically deep convolutional neural networks, have achieved unprecedented performance in various computer vision tasks, but the rationale for the computations and structures of successful neural networks is not fully understood. Theories abound for the aptitude of convolutional neural networks for image classification, but less is understood about why such models would be capable of complex visual tasks such as inference and anomaly identification. Here, we propose a sparse coding interpretation of neural networks that have ReLU activation and of convolutional neural networks in particular. In sparse coding, when the model's basis functions are assumed to be orthogonal, the optimal coefficients are given by the soft-threshold function of the basis functions projected onto the input image. In a non-negative variant of sparse coding, the soft-threshold function becomes a ReLU. Here, we derive these solutions via sparse coding with orthogonal-assumed basis functions, then we derive the convolutional neural network forward transformation from a modified non-negative orthogonal sparse coding model with an exponential prior parameter for each sparse coding coefficient. Next, we derive a complete convolutional neural network without normalization and pooling by adding logistic regression to a hierarchical sparse coding model. Finally we motivate potentially more robust forward transformations by maintaining sparse priors in convolutional neural networks as well performing a stronger nonlinear transformation.

Inference via Sparse Coding in a Hierarchical Vision Model

Sparse coding has been incorporated in models of the visual cortex for its computational advantages and connection to biology. But how the level of sparsity contributes to performance on visual tasks is not well understood. In this work, sparse coding has been integrated into an existing hierarchical V2 model (Hosoya and Hyv\"arinen, 2015), but replacing the Independent Component Analysis (ICA) with an explicit sparse coding in which the degree of sparsity can be controlled. After training, the sparse coding basis functions with a higher degree of sparsity resembled qualitatively different structures, such as curves and corners. The contributions of the models were assessed with image classification tasks, including object classification, and tasks associated with mid-level vision including figure-ground classification, texture classification, and angle prediction between two line stimuli. In addition, the models were assessed in comparison to a texture sensitivity measure that has been reported in V2 (Freeman et al., 2013), and a deleted-region inference task. The results from the experiments show that while sparse coding performed worse than ICA at classifying images, only sparse coding was able to better match the texture sensitivity level of V2 and infer deleted image regions, both by increasing the degree of sparsity in sparse coding. Higher degrees of sparsity allowed for inference over larger deleted image regions. The mechanism that allows for this inference capability in sparse coding is described here.