Quantum Adaptive Fourier Features for Neural Density Estimation

Density estimation is a fundamental task in statistics and machine learning applications. Kernel density estimation is a powerful tool for non-parametric density estimation in low dimensions; however, its performance is poor in higher dimensions. Moreover, its prediction complexity scale linearly with more training data points. This paper presents a method for neural density estimation that can be seen as a type of kernel density estimation, but without the high prediction computational complexity. The method is based on density matrices, a formalism used in quantum mechanics, and adaptive Fourier features. The method can be trained without optimization, but it could be also integrated with deep learning architectures and trained using gradient descent. Thus, it could be seen as a form of neural density estimation method. The method was evaluated in different synthetic and real datasets, and its performance compared against state-of-the-art neural density estimation methods, obtaining competitive results.

Fast Kernel Density Estimation with Density Matrices and Random Fourier Features

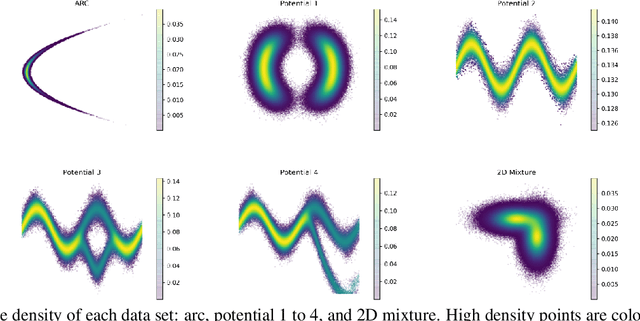
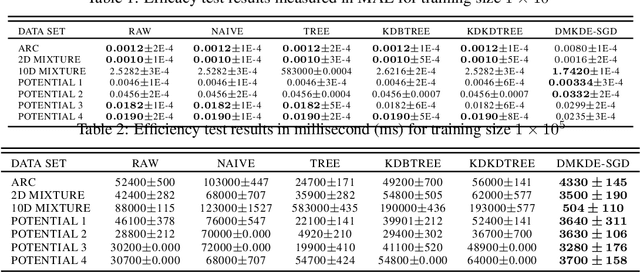
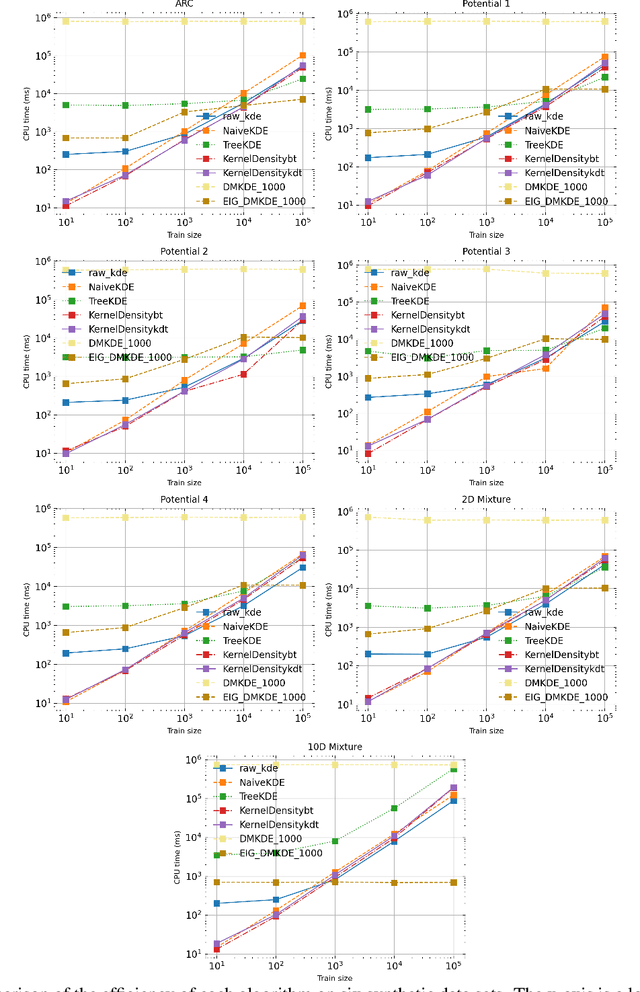
Kernel density estimation (KDE) is one of the most widely used nonparametric density estimation methods. The fact that it is a memory-based method, i.e., it uses the entire training data set for prediction, makes it unsuitable for most current big data applications. Several strategies, such as tree-based or hashing-based estimators, have been proposed to improve the efficiency of the kernel density estimation method. The novel density kernel density estimation method (DMKDE) uses density matrices, a quantum mechanical formalism, and random Fourier features, an explicit kernel approximation, to produce density estimates. This method has its roots in the KDE and can be considered as an approximation method, without its memory-based restriction. In this paper, we systematically evaluate the novel DMKDE algorithm and compare it with other state-of-the-art fast procedures for approximating the kernel density estimation method on different synthetic data sets. Our experimental results show that DMKDE is on par with its competitors for computing density estimates and advantages are shown when performed on high-dimensional data. We have made all the code available as an open source software repository.