Quantum state-agnostic work extraction (almost) without dissipation

We investigate work extraction protocols designed to transfer the maximum possible energy to a battery using sequential access to $N$ copies of an unknown pure qubit state. The core challenge is designing interactions to optimally balance two competing goals: charging of the battery optimally using the qubit in hand, and acquiring more information by qubit to improve energy harvesting in subsequent rounds. Here, we leverage exploration-exploitation trade-off in reinforcement learning to develop adaptive strategies achieving energy dissipation that scales only poly-logarithmically in $N$. This represents an exponential improvement over current protocols based on full state tomography.

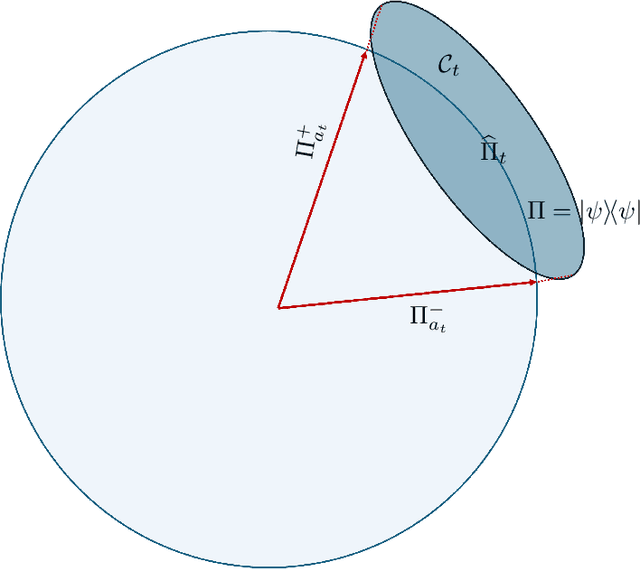
Learning pure quantum states (almost) without regret

We initiate the study of quantum state tomography with minimal regret. A learner has sequential oracle access to an unknown pure quantum state, and in each round selects a pure probe state. Regret is incurred if the unknown state is measured orthogonal to this probe, and the learner's goal is to minimise the expected cumulative regret over $T$ rounds. The challenge is to find a balance between the most informative measurements and measurements incurring minimal regret. We show that the cumulative regret scales as $\Theta(\operatorname{polylog} T)$ using a new tomography algorithm based on a median of means least squares estimator. This algorithm employs measurements biased towards the unknown state and produces online estimates that are optimal (up to logarithmic terms) in the number of observed samples.

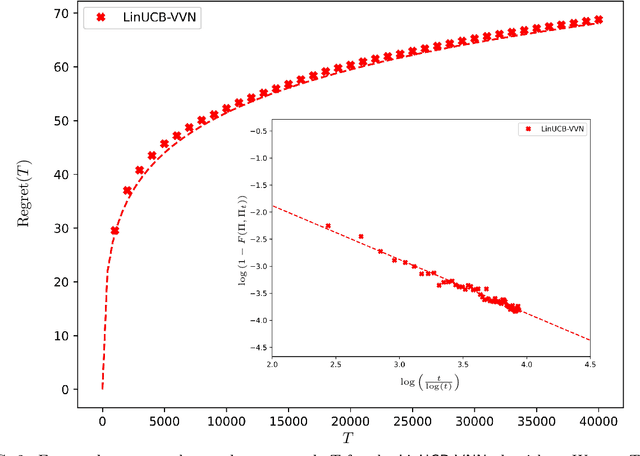
Linear bandits with polylogarithmic minimax regret

We study a noise model for linear stochastic bandits for which the subgaussian noise parameter vanishes linearly as we select actions on the unit sphere closer and closer to the unknown vector. We introduce an algorithm for this problem that exhibits a minimax regret scaling as $\log^3(T)$ in the time horizon $T$, in stark contrast the square root scaling of this regret for typical bandit algorithms. Our strategy, based on weighted least-squares estimation, achieves the eigenvalue relation $\lambda_{\min} ( V_t ) = \Omega (\sqrt{\lambda_{\max}(V_t ) })$ for the design matrix $V_t$ at each time step $t$ through geometrical arguments that are independent of the noise model and might be of independent interest. This allows us to tightly control the expected regret in each time step to be of the order $O(\frac1{t})$, leading to the logarithmic scaling of the cumulative regret.

Learning finitely correlated states: stability of the spectral reconstruction

We show that marginals of subchains of length $t$ of any finitely correlated translation invariant state on a chain can be learned, in trace distance, with $O(t^2)$ copies -- with an explicit dependence on local dimension, memory dimension and spectral properties of a certain map constructed from the state -- and computational complexity polynomial in $t$. The algorithm requires only the estimation of a marginal of a controlled size, in the worst case bounded by a multiple of the minimum bond dimension, from which it reconstructs a translation invariant matrix product operator. In the analysis, a central role is played by the theory of operator systems. A refined error bound can be proven for $C^*$-finitely correlated states, which have an operational interpretation in terms of sequential quantum channels applied to the memory system. We can also obtain an analogous error bound for a class of matrix product density operators reconstructible by local marginals. In this case, a linear number of marginals must be estimated, obtaining a sample complexity of $\tilde{O}(t^3)$. The learning algorithm also works for states that are only close to a finitely correlated state, with the potential of providing competitive algorithms for other interesting families of states.

Quantum contextual bandits and recommender systems for quantum data

We study a recommender system for quantum data using the linear contextual bandit framework. In each round, a learner receives an observable (the context) and has to recommend from a finite set of unknown quantum states (the actions) which one to measure. The learner has the goal of maximizing the reward in each round, that is the outcome of the measurement on the unknown state. Using this model we formulate the low energy quantum state recommendation problem where the context is a Hamiltonian and the goal is to recommend the state with the lowest energy. For this task, we study two families of contexts: the Ising model and a generalized cluster model. We observe that if we interpret the actions as different phases of the models then the recommendation is done by classifying the correct phase of the given Hamiltonian and the strategy can be interpreted as an online quantum phase classifier.