Jos'e Vin'icius de M. Cardoso
Structured Graph Learning Via Laplacian Spectral Constraints
Sep 24, 2019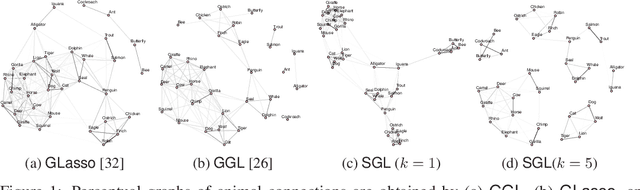

Abstract:Learning a graph with a specific structure is essential for interpretability and identification of the relationships among data. It is well known that structured graph learning from observed samples is an NP-hard combinatorial problem. In this paper, we first show that for a set of important graph families it is possible to convert the structural constraints of structure into eigenvalue constraints of the graph Laplacian matrix. Then we introduce a unified graph learning framework, lying at the integration of the spectral properties of the Laplacian matrix with Gaussian graphical modeling that is capable of learning structures of a large class of graph families. The proposed algorithms are provably convergent and practically amenable for large-scale semi-supervised and unsupervised graph-based learning tasks. Extensive numerical experiments with both synthetic and real data sets demonstrate the effectiveness of the proposed methods. An R package containing code for all the experimental results is available at https://cran.r-project.org/package=spectralGraphTopology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge