Graph topology inference with derivative-reproducing property in RKHS: algorithm and convergence analysis

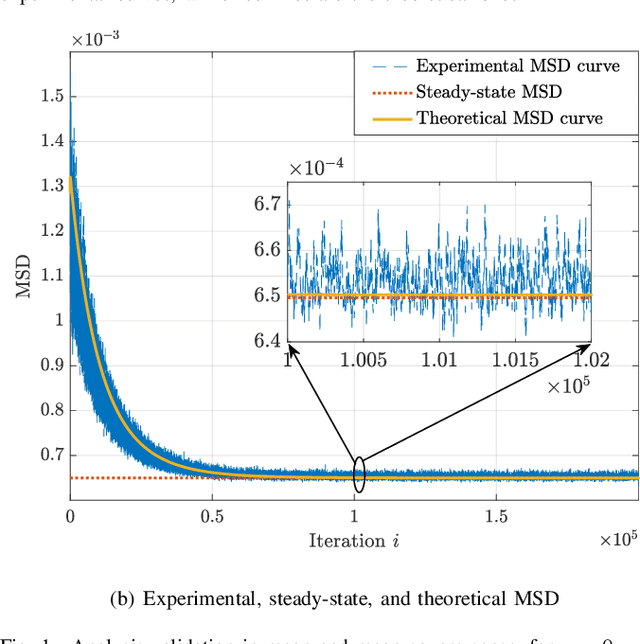
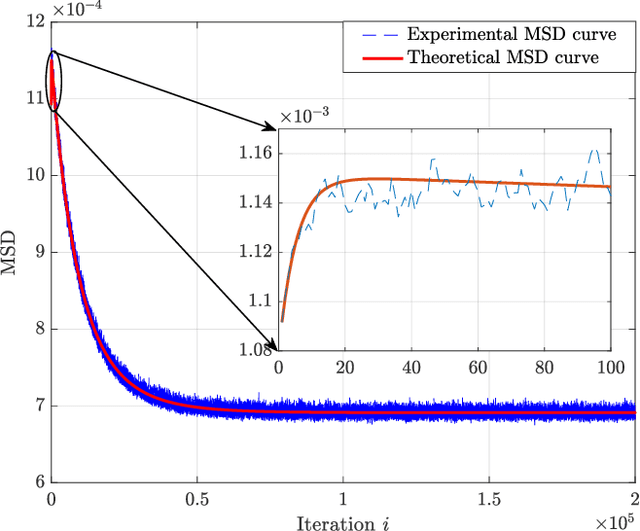
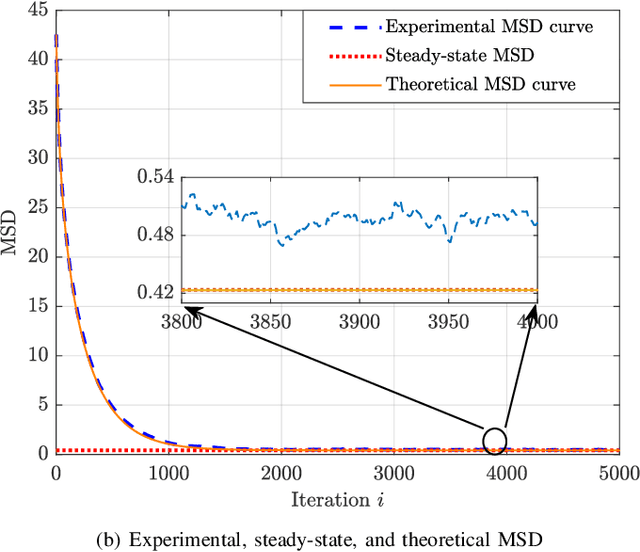
In many areas such as computational biology, finance or social sciences, knowledge of an underlying graph explaining the interactions between agents is of paramount importance but still challenging. Considering that these interactions may be based on nonlinear relationships adds further complexity to the topology inference problem. Among the latest methods that respond to this need is a topology inference one proposed by the authors, which estimates a possibly directed adjacency matrix in an online manner. Contrasting with previous approaches based on linear models, the considered model is able to explain nonlinear interactions between the agents in a network. The novelty in the considered method is the use of a derivative-reproducing property to enforce network sparsity, while reproducing kernels are used to model the nonlinear interactions. The aim of this paper is to present a thorough convergence analysis of this method. The analysis is proven to be sane both in the mean and mean square sense. In addition, stability conditions are devised to ensure the convergence of the analyzed method.