Exact Matching in Correlated Networks with Node Attributes for Improved Community Recovery

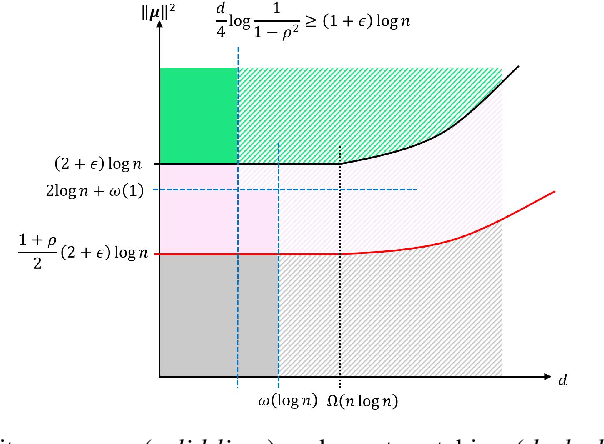
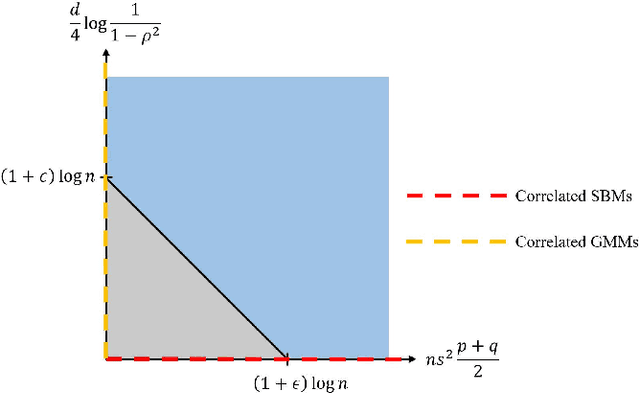
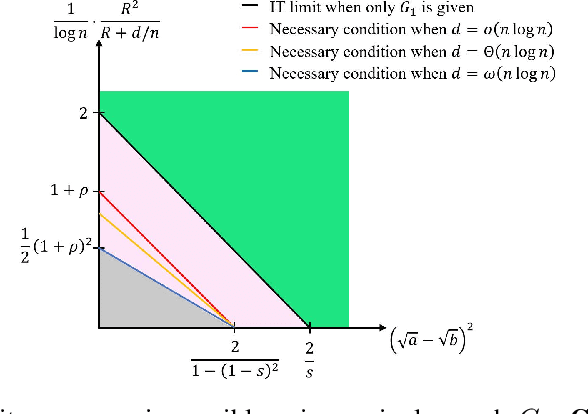
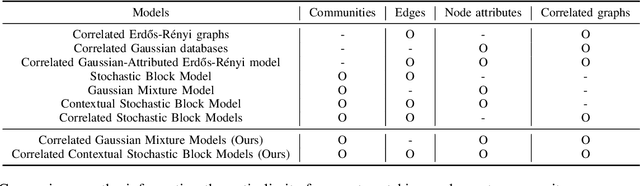
We study community detection in multiple networks whose nodes and edges are jointly correlated. This setting arises naturally in applications such as social platforms, where a shared set of users may exhibit both correlated friendship patterns and correlated attributes across different platforms. Extending the classical Stochastic Block Model (SBM) and its contextual counterpart (CSBM), we introduce the correlated CSBM, which incorporates structural and attribute correlations across graphs. To build intuition, we first analyze correlated Gaussian Mixture Models, wherein only correlated node attributes are available without edges, and identify the conditions under which an estimator minimizing the distance between attributes achieves exact matching of nodes across the two databases. For correlated CSBMs, we develop a two-step procedure that first applies $k$-core matching to most nodes using edge information, then refines the matching for the remaining unmatched nodes by leveraging their attributes with a distance-based estimator. We identify the conditions under which the algorithm recovers the exact node correspondence, enabling us to merge the correlated edges and average the correlated attributes for enhanced community detection. Crucially, by aligning and combining graphs, we identify regimes in which community detection is impossible in a single graph but becomes feasible when side information from correlated graphs is incorporated. Our results illustrate how the interplay between graph matching and community recovery can boost performance, broadening the scope of multi-graph, attribute-based community detection.

Efficient Algorithms for Exact Graph Matching on Correlated Stochastic Block Models with Constant Correlation

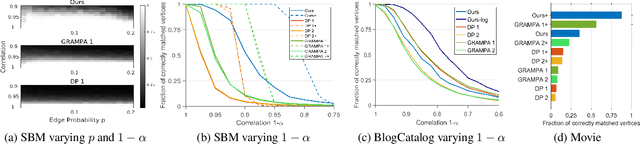
We consider the problem of graph matching, or learning vertex correspondence, between two correlated stochastic block models (SBMs). The graph matching problem arises in various fields, including computer vision, natural language processing and bioinformatics, and in particular, matching graphs with inherent community structure has significance related to de-anonymization of correlated social networks. Compared to the correlated Erdos-Renyi (ER) model, where various efficient algorithms have been developed, among which a few algorithms have been proven to achieve the exact matching with constant edge correlation, no low-order polynomial algorithm has been known to achieve exact matching for the correlated SBMs with constant correlation. In this work, we propose an efficient algorithm for matching graphs with community structure, based on the comparison between partition trees rooted from each vertex, by extending the idea of Mao et al. (2021) to graphs with communities. The partition tree divides the large neighborhoods of each vertex into disjoint subsets using their edge statistics to different communities. Our algorithm is the first low-order polynomial-time algorithm achieving exact matching between two correlated SBMs with high probability in dense graphs.