Non-binary artificial neuron with phase variation implemented on a quantum computer

The first artificial quantum neuron models followed a similar path to classic models, as they work only with discrete values. Here we introduce an algorithm that generalizes the binary model manipulating the phase of complex numbers. We propose, test, and implement a neuron model that works with continuous values in a quantum computer. Through simulations, we demonstrate that our model may work in a hybrid training scheme utilizing gradient descent as a learning algorithm. This work represents another step in the direction of evaluation of the use of artificial neural networks efficiently implemented on near-term quantum devices.

Hybrid model of the kernel method for quantum computers

The field of quantum machine learning is a promising way to lead to a revolution in intelligent data processing methods. In this way, a hybrid learning method based on classic kernel methods is proposed. This proposal also requires the development of a quantum algorithm for the calculation of internal products between vectors of continuous values. In order for this to be possible, it was necessary to make adaptations to the classic kernel method, since it is necessary to consider the limitations imposed by the Hilbert space of the quantum processor. As a test case, we applied this new algorithm to learn to classify whether new points generated randomly, in a finite square located under a plane, were found inside or outside a circle located inside this square. It was found that the algorithm was able to correctly detect new points in 99% of the samples tested, with a small difference due to considering the radius slightly larger than the ideal. However, the kernel method was able to perform classifications correctly, as well as the internal product algorithm successfully performed the internal product calculations using quantum resources. Thus, the present work represents a contribution to the area, proposing a new model of machine learning accessible to both physicists and computer scientists.

QuForge: A Library for Qudits Simulation

Quantum computing with qudits, an extension of qubits to multiple levels, is a research field less mature than qubit-based quantum computing. However, qudits can offer some advantages over qubits, by representing information with fewer separated components. In this article, we present QuForge, a Python-based library designed to simulate quantum circuits with qudits. This library provides the necessary quantum gates for implementing quantum algorithms, tailored to any chosen qudit dimension. Built on top of differentiable frameworks, QuForge supports execution on accelerating devices such as GPUs and TPUs, significantly speeding up simulations. It also supports sparse operations, leading to a reduction in memory consumption compared to other libraries. Additionally, by constructing quantum circuits as differentiable graphs, QuForge facilitates the implementation of quantum machine learning algorithms, enhancing the capabilities and flexibility of quantum computing research.

Barren plateaus induced by the dimension of qudits

Variational Quantum Algorithms (VQAs) have emerged as pivotal strategies for attaining quantum advantages in diverse scientific and technological domains, notably within Quantum Neural Networks. However, despite their potential, VQAs encounter significant obstacles, chief among them being the gradient vanishing problem, commonly referred to as barren plateaus. In this study, we unveil a direct correlation between the dimension of qudits and the occurrence of barren plateaus, a connection previously overlooked. Through meticulous analysis, we demonstrate that existing literature implicitly suggests the intrinsic influence of qudit dimensionality on barren plateaus. To instantiate these findings, we present numerical results that exemplify the impact of qudit dimensionality on barren plateaus. Additionally, despite the proposition of various error mitigation techniques, our results call for further scrutiny about their efficacy in the context of VQAs with qudits.

Quantum neural network with ensemble learning to mitigate barren plateaus and cost function concentration

The rapid development of quantum computers promises transformative impacts across diverse fields of science and technology. Quantum neural networks (QNNs), as a forefront application, hold substantial potential. Despite the multitude of proposed models in the literature, persistent challenges, notably the vanishing gradient (VG) and cost function concentration (CFC) problems, impede their widespread success. In this study, we introduce a novel approach to quantum neural network construction, specifically addressing the issues of VG and CFC. Our methodology employs ensemble learning, advocating for the simultaneous deployment of multiple quantum circuits with a depth equal to $1$, a departure from the conventional use of a single quantum circuit with depth $L$. We assess the efficacy of our proposed model through a comparative analysis with a conventionally constructed QNN. The evaluation unfolds in the context of a classification problem, yielding valuable insights into the potential advantages of our innovative approach.

A differentiable programming framework for spin models

Spin systems are a powerful tool for modeling a wide range of physical systems. In this paper, we propose a novel framework for modeling spin systems using differentiable programming. Our approach enables us to efficiently simulate spin systems, making it possible to model complex systems at scale. Specifically, we demonstrate the effectiveness of our technique by applying it to three different spin systems: the Ising model, the Potts model, and the Cellular Potts model. Our simulations show that our framework offers significant speedup compared to traditional simulation methods, thanks to its ability to execute code efficiently across different hardware architectures, including Graphical Processing Units and Tensor Processing Units.

The quantum cost function concentration dependency on the parametrization expressivity

Although we are currently in the era of noisy intermediate scale quantum devices, several studies are being conducted with the aim of bringing machine learning to the quantum domain. Currently, quantum variational circuits are one of the main strategies used to build such models. However, despite its widespread use, we still do not know what are the minimum resources needed to create a quantum machine learning model. In this article, we analyze how the expressiveness of the parametrization affects the cost function. We analytically show that the more expressive the parametrization is, the more the cost function will tend to concentrate around a value that depends both on the chosen observable and on the number of qubits used. For this, we initially obtain a relationship between the expressiveness of the parametrization and the mean value of the cost function. Afterwards, we relate the expressivity of the parametrization with the variance of the cost function. Finally, we show some numerical simulation results that confirm our theoretical-analytical predictions.

Restricting to the chip architecture maintains the quantum neural network accuracy, if the parameterization is a $2$-design

In the era of noisy intermediate scale quantum devices, variational quantum circuits (VQCs) are currently one of the main strategies for building quantum machine learning models. These models are made up of a quantum part and a classical part. The quantum part is given by a parametrization $U$, which, in general, is obtained from the product of different quantum gates. By its turn, the classical part corresponds to an optimizer that updates the parameters of $U$ in order to minimize a cost function $C$. However, despite the many applications of VQCs, there are still questions to be answered, such as for example: What is the best sequence of gates to be used? How to optimize their parameters? Which cost function to use? How the architecture of the quantum chips influences the final results? In this article, we focus on answering the last question. We will show that, in general, the cost function will tend to a typical average value the closer the parameterization used is from a $2$-design. Therefore, the closer this parameterization is to a $2$-design, the less the result of the quantum neural network model will depend on its parametrization. As a consequence, we can use the own architecture of the quantum chips to defined the VQC parametrization, avoiding the use of additional swap gates and thus diminishing the VQC depth and the associated errors.

Avoiding Barren Plateaus with Classical Deep Neural Networks

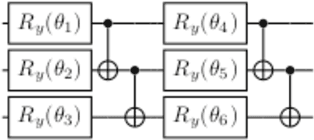
Variational quantum algorithms (VQAs) are among the most promising algorithms in the era of Noisy Intermediate Scale Quantum Devices. The VQAs are applied to a variety of tasks, such as in chemistry simulations, optimization problems, and quantum neural networks. Such algorithms are constructed using a parameterization U($\pmb{\theta}$) with a classical optimizer that updates the parameters $\pmb{\theta}$ in order to minimize a cost function $C$. For this task, in general the gradient descent method, or one of its variants, is used. This is a method where the circuit parameters are updated iteratively using the cost function gradient. However, several works in the literature have shown that this method suffers from a phenomenon known as the Barren Plateaus (BP). This phenomenon is characterized by the exponentially flattening of the cost function landscape, so that the number of times the function must be evaluated to perform the optimization grows exponentially as the number of qubits and parameterization depth increase. In this article, we report on how the use of a classical neural networks in the VQAs input parameters can alleviate the BP phenomenon.

Natural evolutionary strategies applied to quantum-classical hybrid neural networks

With the rapid development of quantum computers, several applications are being proposed for them. Quantum simulations, simulation of chemical reactions, solution of optimization problems and quantum neural networks are some examples. However, problems such as noise, limited number of qubits and circuit depth, and gradient vanishing must be resolved before we can use them to their full potential. In the field of quantum machine learning, several models have been proposed. In general, in order to train these different models, we use the gradient of a cost function with respect to the model parameters. In order to obtain this gradient, we must compute the derivative of this function with respect to the model parameters. For this we can use the method called parameter-shift rule. This method consists of evaluating the cost function twice for each parameter of the quantum network. A problem with this method is that the number of evaluations grows linearly with the number of parameters. In this work we study an alternative method, called Natural Evolutionary Strategies (NES), which are a family of black box optimization algorithms. An advantage of the NES method is that in using it one can control the number of times the cost function will be evaluated. We apply the NES method to the binary classification task, showing that this method is a viable alternative for training quantum neural networks.