Avoiding Barren Plateaus with Classical Deep Neural Networks

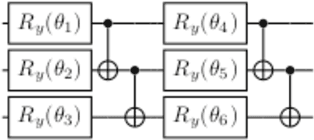
Variational quantum algorithms (VQAs) are among the most promising algorithms in the era of Noisy Intermediate Scale Quantum Devices. The VQAs are applied to a variety of tasks, such as in chemistry simulations, optimization problems, and quantum neural networks. Such algorithms are constructed using a parameterization U($\pmb{\theta}$) with a classical optimizer that updates the parameters $\pmb{\theta}$ in order to minimize a cost function $C$. For this task, in general the gradient descent method, or one of its variants, is used. This is a method where the circuit parameters are updated iteratively using the cost function gradient. However, several works in the literature have shown that this method suffers from a phenomenon known as the Barren Plateaus (BP). This phenomenon is characterized by the exponentially flattening of the cost function landscape, so that the number of times the function must be evaluated to perform the optimization grows exponentially as the number of qubits and parameterization depth increase. In this article, we report on how the use of a classical neural networks in the VQAs input parameters can alleviate the BP phenomenon.