Dataflow Matrix Machines and V-values: a Bridge between Programs and Neural Nets

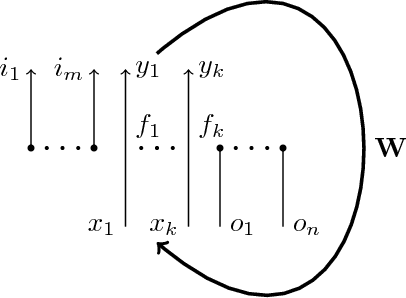
1) Dataflow matrix machines (DMMs) generalize neural nets by replacing streams of numbers with linear streams (streams supporting linear combinations), allowing arbitrary input and output arities for activation functions, countable-sized networks with finite dynamically changeable active part capable of unbounded growth, and a very expressive self-referential mechanism. 2) DMMs are suitable for general-purpose programming, while retaining the key property of recurrent neural networks: programs are expressed via matrices of real numbers, and continuous changes to those matrices produce arbitrarily small variations in the associated programs. 3) Spaces of V-values (vector-like elements based on nested maps) are particularly useful, enabling DMMs with variadic activation functions and conveniently representing conventional data structures.

Dataflow Matrix Machines as a Model of Computations with Linear Streams

We overview dataflow matrix machines as a Turing complete generalization of recurrent neural networks and as a programming platform. We describe vector space of finite prefix trees with numerical leaves which allows us to combine expressive power of dataflow matrix machines with simplicity of traditional recurrent neural networks.