John C. Raisbeck
Massachusetts General Hospital
Agent Spaces
Nov 11, 2021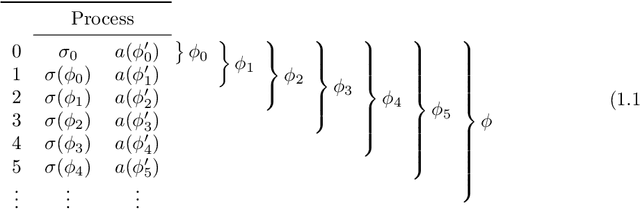

Abstract:Exploration is one of the most important tasks in Reinforcement Learning, but it is not well-defined beyond finite problems in the Dynamic Programming paradigm (see Subsection 2.4). We provide a reinterpretation of exploration which can be applied to any online learning method. We come to this definition by approaching exploration from a new direction. After finding that concepts of exploration created to solve simple Markov decision processes with Dynamic Programming are no longer broadly applicable, we reexamine exploration. Instead of extending the ends of dynamic exploration procedures, we extend their means. That is, rather than repeatedly sampling every state-action pair possible in a process, we define the act of modifying an agent to itself be explorative. The resulting definition of exploration can be applied in infinite problems and non-dynamic learning methods, which the dynamic notion of exploration cannot tolerate. To understand the way that modifications of an agent affect learning, we describe a novel structure on the set of agents: a collection of distances (see footnote 7) $d_{a} \in A$, which represent the perspectives of each agent possible in the process. Using these distances, we define a topology and show that many important structures in Reinforcement Learning are well behaved under the topology induced by convergence in the agent space.
Evolution Strategies Converges to Finite Differences
Dec 27, 2019Abstract:Since the debut of Evolution Strategies (ES) as a tool for Reinforcement Learning by Salimans et al. 2017, there has been interest in determining the exact relationship between the Evolution Strategies gradient and the gradient of a similar class of algorithms, Finite Differences (FD).(Zhang et al. 2017, Lehman et al. 2018) Several investigations into the subject have been performed, investigating the formal motivational differences(Lehman et al. 2018) between ES and FD, as well as the differences in a standard benchmark problem in Machine Learning, the MNIST classification problem(Zhang et al. 2017). This paper proves that while the gradients are different, they converge as the dimension of the vector under optimization increases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge