Coefficients' Settings in Particle Swarm Optimization: Insight and Guidelines

Particle Swam Optimization is a population-based and gradient-free optimization method developed by mimicking social behaviour observed in nature. Its ability to optimize is not specifically implemented but emerges in the global level from local interactions. In its canonical version, there are three factors that govern a particle's trajectory: 1) inertia from its previous displacement; 2) attraction to its best experience; and 3) attraction to a given neighbour's best experience. The importance given to each of these factors is regulated by three coefficients: 1) the inertia; 2) the individuality; and 3) the sociality weights. Their settings rule the trajectory of the particle when pulled by these two attractors. Different speeds and forms of convergence of a particle towards its attractor(s) take place for different settings of the coefficients. A more general formulation is presented aiming for a better control of the embedded randomness. Guidelines to select the coefficients' settings to obtain the desired behaviour are offered. The convergence speed of the algorithm also depends on the speed of spread of information within the swarm. The latter is governed by the structure of the neighbourhood, whose study is beyond the scope of this paper. The objective here is to help understand the core of the PSO paradigm from the bottom up by offering some insight into the form of the particles' trajectories, and to provide some guidelines as to how to decide upon the settings of the coefficients in the particles' velocity update equation in the proposed formulation to obtain the type of behaviour desired for the problem at hand. General-purpose settings are also suggested. The relationship between the proposed formulation and both the classical and constricted PSO formulations are also provided.

Pseudo-Adaptive Penalization to Handle Constraints in Particle Swarm Optimizers

The penalization method is a popular technique to provide particle swarm optimizers with the ability to handle constraints. The downside is the need of penalization coefficients whose settings are problem-specific. While adaptive coefficients can be found in the literature, a different adaptive scheme is proposed in this paper, where coefficients are kept constant. A pseudo-adaptive relaxation of the tolerances for constraint violations while penalizing only violations beyond such tolerances results in a pseudo-adaptive penalization. A particle swarm optimizer is tested on a suite of benchmark problems for three types of tolerance relaxation: no relaxation; self-tuned initial relaxation with deterministic decrease; and self-tuned initial relaxation with pseudo-adaptive decrease. Other authors' results are offered as frames of reference.

Individual and Social Behaviour in Particle Swarm Optimizers

Three basic factors govern the individual behaviour of a particle: the inertia from its previous displacement; the attraction to its own best experience; and the attraction to a given neighbour's best experience. The importance awarded to each factor is controlled by three coefficients: the inertia; the individuality; and the sociality weights. The social behaviour is ruled by the structure of the social network, which defines the neighbours that are to inform of their experiences to a given particle. This paper presents a study of the influence of different settings of the coefficients as well as of the combined effect of different settings and different neighbourhood topologies on the speed and form of convergence.

Combining Particle Swarm Optimizer with SQP Local Search for Constrained Optimization Problems

The combining of a General-Purpose Particle Swarm Optimizer (GP-PSO) with Sequential Quadratic Programming (SQP) algorithm for constrained optimization problems has been shown to be highly beneficial to the refinement, and in some cases, the success of finding a global optimum solution. It is shown that the likely difference between leading algorithms are in their local search ability. A comparison with other leading optimizers on the tested benchmark suite, indicate the hybrid GP-PSO with implemented local search to compete along side other leading PSO algorithms.

Numerical Comparison of Neighbourhood Topologies in Particle Swarm Optimization

Particle Swarm Optimization is a global optimizer in the sense that it has the ability to escape poor local optima. However, if the spread of information within the population is not adequately performed, premature convergence may occur. The convergence speed and hence the reluctance of the algorithm to getting trapped in suboptimal solutions are controlled by the settings of the coefficients in the velocity update equation as well as by the neighbourhood topology. The coefficients settings govern the trajectories of the particles towards the good locations identified, whereas the neighbourhood topology controls the form and speed of spread of information within the population (i.e. the update of the social attractor). Numerous neighbourhood topologies have been proposed and implemented in the literature. This paper offers a numerical comparison of the performances exhibited by five different neighbourhood topologies combined with four different coefficients' settings when optimizing a set of benchmark unconstrained problems. Despite the optimum topology being problem-dependent, it appears that dynamic neighbourhoods with the number of interconnections increasing as the search progresses should be preferred for a non-problem-specific optimizer.

Particle Swarm Optimization: Fundamental Study and its Application to Optimization and to Jetty Scheduling Problems

The advantages of evolutionary algorithms with respect to traditional methods have been greatly discussed in the literature. While particle swarm optimizers share such advantages, they outperform evolutionary algorithms in that they require lower computational cost and easier implementation, involving no operator design and few coefficients to be tuned. However, even marginal variations in the settings of these coefficients greatly influence the dynamics of the swarm. Since this paper does not intend to study their tuning, general-purpose settings are taken from previous studies, and virtually the same algorithm is used to optimize a variety of notably different problems. Thus, following a review of the paradigm, the algorithm is tested on a set of benchmark functions and engineering problems taken from the literature. Later, complementary lines of code are incorporated to adapt the method to combinatorial optimization as it occurs in scheduling problems, and a real case is solved using the same optimizer with the same settings. The aim is to show the flexibility and robustness of the approach, which can handle a wide variety of problems.

Constraint-Handling Techniques for Particle Swarm Optimization Algorithms

Population-based methods can cope with a variety of different problems, including problems of remarkably higher complexity than those traditional methods can handle. The main procedure consists of successively updating a population of candidate solutions, performing a parallel exploration instead of traditional sequential exploration. While the origins of the PSO method are linked to bird flock simulations, it is a stochastic optimization method in the sense that it relies on random coefficients to introduce creativity, and a bottom-up artificial intelligence-based approach in the sense that its intelligent behaviour emerges in a higher level than the individuals' rather than deterministically programmed. As opposed to EAs, the PSO involves no operator design and few coefficients to be tuned. Since this paper does not intend to study such tuning, general-purpose settings are taken from previous studies. The PSO algorithm requires the incorporation of some technique to handle constraints. A popular one is the penalization method, which turns the original constrained problem into unconstrained by penalizing infeasible solutions. Other techniques can be specifically designed for PSO. Since these strategies present advantages and disadvantages when compared to one another, there is no obvious best constraint-handling technique (CHT) for all problems. The aim here is to develop and compare different CHTs suitable for PSOs, which are incorporated to an algorithm with general-purpose settings. The comparisons are performed keeping the remaining features of the algorithm the same, while comparisons to other authors' results are offered as a frame of reference for the optimizer as a whole. Thus, the penalization, preserving feasibility and bisection methods are discussed, implemented, and tested on two suites of benchmark problems. Three neighbourhood sizes are also considered in the experiments.

A Study of the Fundamental Parameters of Particle Swarm Optimizers

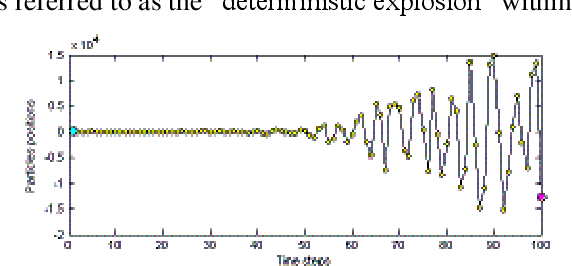
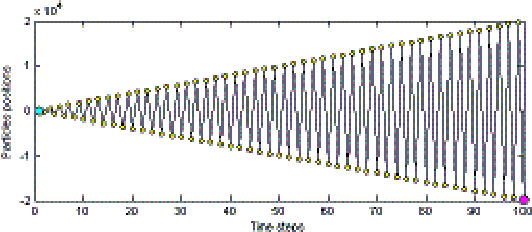
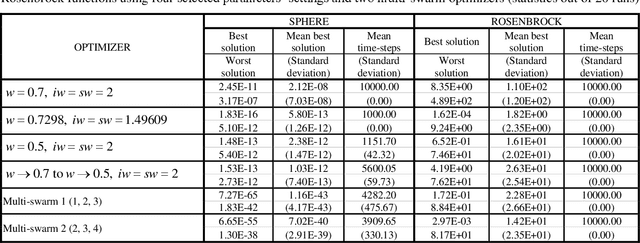
The range of applications of traditional optimization methods are limited by the features of the object variables, and of both the objective and the constraint functions. In contrast, population-based algorithms whose optimization capabilities are emergent properties, such as evolutionary algorithms and particle swarm optimization, present almost no restriction on those features and can handle different optimization problems with few or no adaptations. Their main drawbacks consist of their comparatively higher computational cost and difficulty in handling equality constraints. The particle swarm optimization method is sometimes viewed as an evolutionary algorithm because of their many similarities, despite not being inspired by the same metaphor: they evolve a population of individuals taking into account previous experiences and using stochastic operators to introduce new responses. The advantages of evolutionary algorithms with respect to traditional methods have been greatly discussed in the literature for decades. While the particle swarm optimizers share such advantages, their main desirable features when compared to evolutionary algorithms are their lower computational cost and easier implementation, involving no operator design and few parameters to be tuned. However, even slight modifications of these parameters greatly influence the dynamics of the swarm. This paper deals with the effect of the settings of the parameters of the particles' velocity update equation on the behaviour of the system.

Particle Swarm Optimization: Development of a General-Purpose Optimizer

Traditional methods present a very restrictive range of applications, mainly limited by the features of the function to be optimized and of the constraint functions. In contrast, evolutionary algorithms present almost no restriction to the features of these functions, although the most appropriate constraint-handling technique is still an open question. The particle swarm optimization (PSO) method is sometimes viewed as another evolutionary algorithm because of their many similarities, despite not being inspired by the same metaphor. Namely, they evolve a population of individuals taking into consideration previous experiences and using stochastic operators to introduce new responses. The advantages of evolutionary algorithms with respect to traditional methods have been greatly discussed in the literature for decades. While all such advantages are valid when comparing the PSO paradigm to traditional methods, its main advantages with respect to evolutionary algorithms consist of its noticeably lower computational cost and easier implementation. In fact, the plain version can be programmed in a few lines of code, involving no operator design and few parameters to be tuned. This paper deals with three important aspects of the method: the influence of the parameters' tuning on the behaviour of the system; the design of stopping criteria so that the reliability of the solution found can be somehow estimated and computational cost can be saved; and the development of appropriate techniques to handle constraints, given that the original method is designed for unconstrained optimization problems.