A Study of the Fundamental Parameters of Particle Swarm Optimizers
Paper and Code
Jan 25, 2021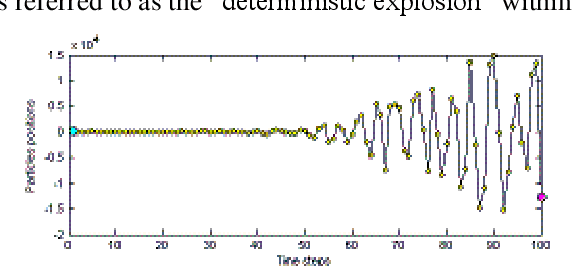

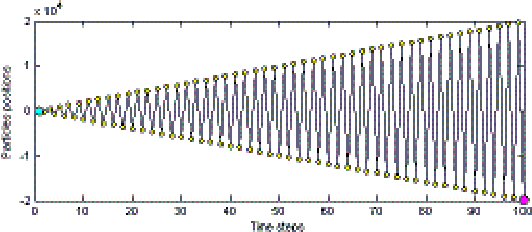
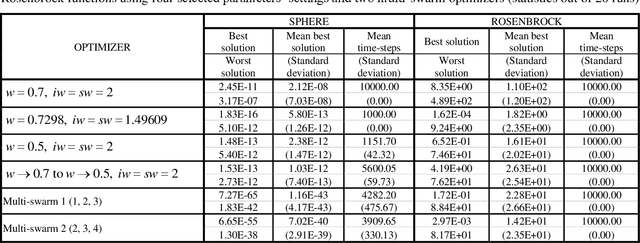
The range of applications of traditional optimization methods are limited by the features of the object variables, and of both the objective and the constraint functions. In contrast, population-based algorithms whose optimization capabilities are emergent properties, such as evolutionary algorithms and particle swarm optimization, present almost no restriction on those features and can handle different optimization problems with few or no adaptations. Their main drawbacks consist of their comparatively higher computational cost and difficulty in handling equality constraints. The particle swarm optimization method is sometimes viewed as an evolutionary algorithm because of their many similarities, despite not being inspired by the same metaphor: they evolve a population of individuals taking into account previous experiences and using stochastic operators to introduce new responses. The advantages of evolutionary algorithms with respect to traditional methods have been greatly discussed in the literature for decades. While the particle swarm optimizers share such advantages, their main desirable features when compared to evolutionary algorithms are their lower computational cost and easier implementation, involving no operator design and few parameters to be tuned. However, even slight modifications of these parameters greatly influence the dynamics of the swarm. This paper deals with the effect of the settings of the parameters of the particles' velocity update equation on the behaviour of the system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge