Johan Leduc
Generative Modeling of Complex Data
Feb 04, 2022Abstract:In recent years, several models have improved the capacity to generate synthetic tabular datasets. However, such models focus on synthesizing simple columnar tables and are not useable on real-life data with complex structures. This paper puts forward a generic framework to synthesize more complex data structures with composite and nested types. It then proposes one practical implementation, built with causal transformers, for struct (mappings of types) and lists (repeated instances of a type). The results on standard benchmark datasets show that such implementation consistently outperforms current state-of-the-art models both in terms of machine learning utility and statistical similarity. Moreover, it shows very strong results on two complex hierarchical datasets with multiple nesting and sparse data, that were previously out of reach.
Composable Generative Models
Feb 18, 2021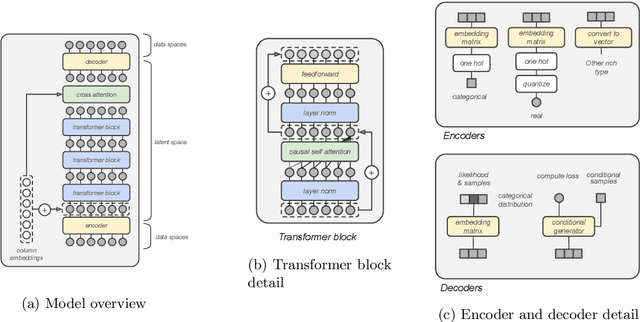
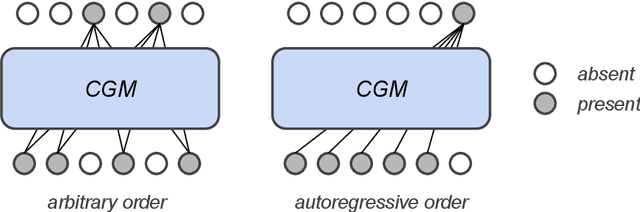
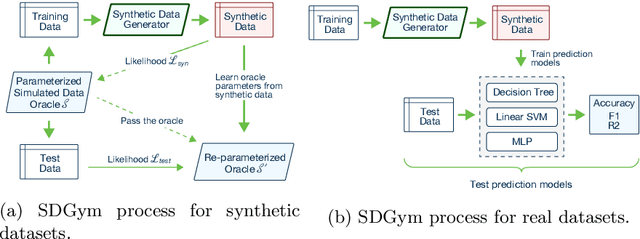
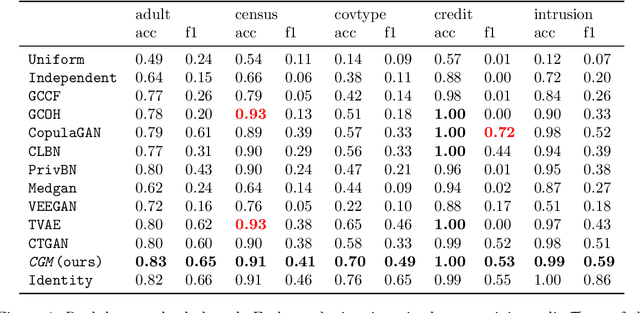
Abstract:Generative modeling has recently seen many exciting developments with the advent of deep generative architectures such as Variational Auto-Encoders (VAE) or Generative Adversarial Networks (GAN). The ability to draw synthetic i.i.d. observations with the same joint probability distribution as a given dataset has a wide range of applications including representation learning, compression or imputation. It appears that it also has many applications in privacy preserving data analysis, especially when used in conjunction with differential privacy techniques. This paper focuses on synthetic data generation models with privacy preserving applications in mind. It introduces a novel architecture, the Composable Generative Model (CGM) that is state-of-the-art in tabular data generation. Any conditional generative model can be used as a sub-component of the CGM, including CGMs themselves, allowing the generation of numerical, categorical data as well as images, text, or time series. The CGM has been evaluated on 13 datasets (6 standard datasets and 7 simulated) and compared to 14 recent generative models. It beats the state of the art in tabular data generation by a significant margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge