Joel A. Hesch
Consistent Map-based 3D Localization on Mobile Devices
Apr 27, 2016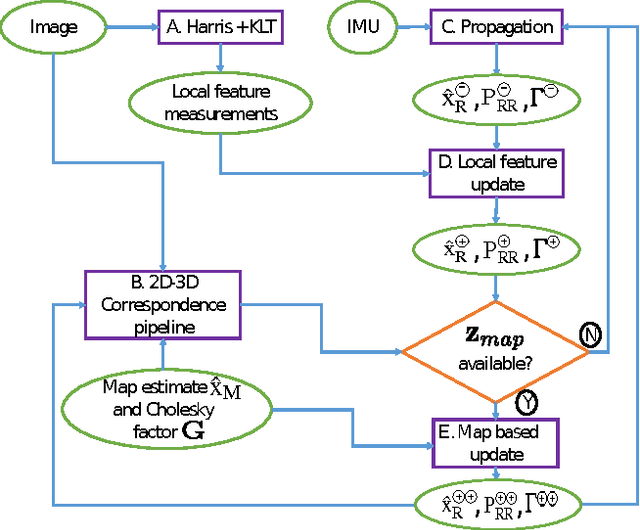
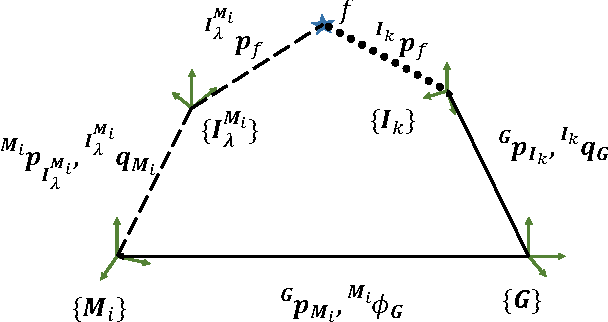
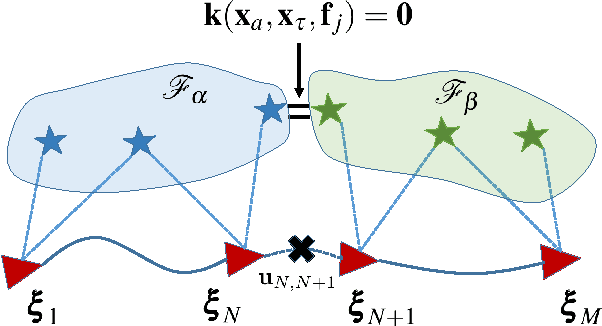
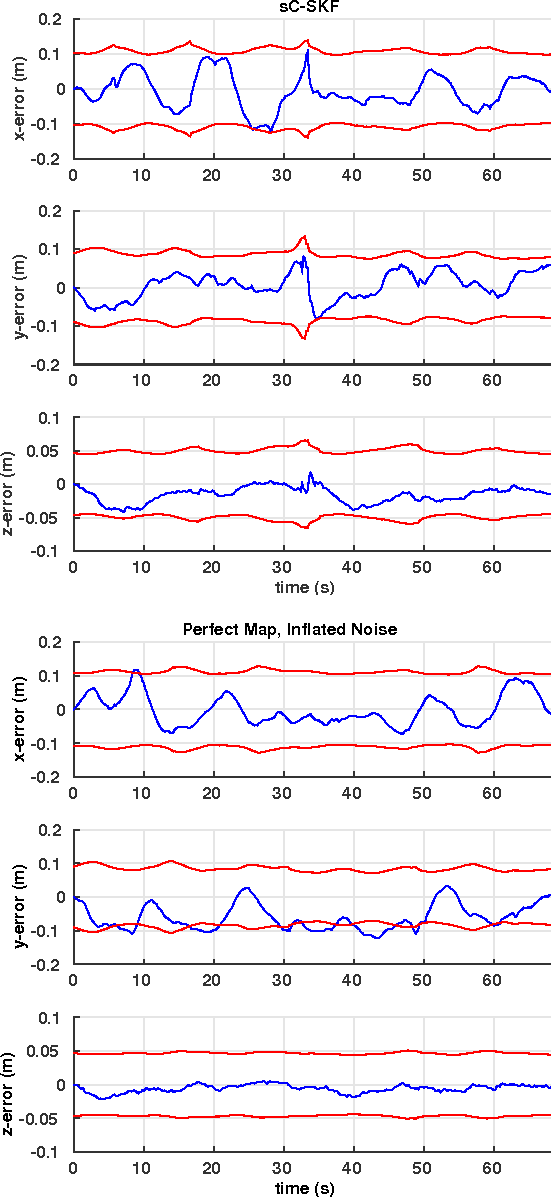
Abstract:The objective of this paper is to provide consistent, real-time 3D localization capabilities to mobile devices navigating within previously mapped areas. To this end, we introduce the Cholesky-Schmidt-Kalman filter (C-SKF), which explicitly considers the uncertainty of the prior map, by employing the sparse Cholesky factor of the map's Hessian, instead of its dense covariance--as is the case for the Schmidt-Kalman filter (SKF). By doing so, the C-SKF has memory requirements typically linear in the size of the map, as opposed to quadratic for storing the map's covariance. Moreover, and in order to bound the processing needs of the C-SKF (between linear and quadratic in the size of the map), we introduce a relaxation of the C-SKF algorithm, the sC-SKF, which operates on the Cholesky factors of independent sub-maps resulting from dividing the trajectory and observations used for constructing the map into overlapping segments. Lastly, we assess the processing and memory requirements of the proposed C-SKF and sC-SKF algorithms, and compare their positioning accuracy against other approximate map-based localization approaches that employ measurement-noise-covariance inflation to compensate for the map's uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge