Uplink Multi-User MIMO Implementation in OpenAirInterface for a Cell-Free O-RAN Testbed

Cell-Free Multiple-Input Multiple-Output (MIMO) and Open Radio Access Network (O-RAN) have been active research topics in the wireless communication community in recent years. As an open-source software implementation of the 3rd Generation Partnership Project (3GPP) 5th Generation (5G) protocol stack, OpenAirInterface (OAI) has become a valuable tool for deploying and testing new ideas in wireless communication systems. In this paper, we present our OAI based real-time uplink Multi-User MIMO (MU-MIMO) testbed developed at Fraunhofer HHI. As a part of our Cell-Free MIMO testbed development, we built a 2x2 MU-MIMO system using general purpose computers and commercially available software defined radios (SDRs). Using a modified OAI next-Generation Node-B (gNB) and two unmodified OAI user equipment (UE), we show that it is feasible to use Sounding Reference Signal (SRS) channel estimates to compute uplink combiners. Our results verify that this method can be used to separate and decode signals from two users transmitting in nonorthogonal time-frequency resources. This work serves as an important verification step to build a complete Cell-Free MU-MIMO system that leverages time domain duplexing (TDD) reciprocity to do downlink beamforming over multiple cells.

Optimized Detection with Analog Beamforming for Monostatic Integrated Sensing and Communication

In this paper, we formalize an optimization framework for analog beamforming in the context of monostatic integrated sensing and communication (ISAC), where we also address the problem of self-interference in the analog domain. As a result, we derive semidefinite programs to approach detection-optimal transmit and receive beamformers, and we devise a superiorized iterative projection algorithm to approximate them. Our simulations show that this approach outperforms the detection performance of well-known design techniques for ISAC beamforming, while it achieves satisfactory self-interference suppression.

Superiorized Adaptive Projected Subgradient Method with Application to MIMO Detection

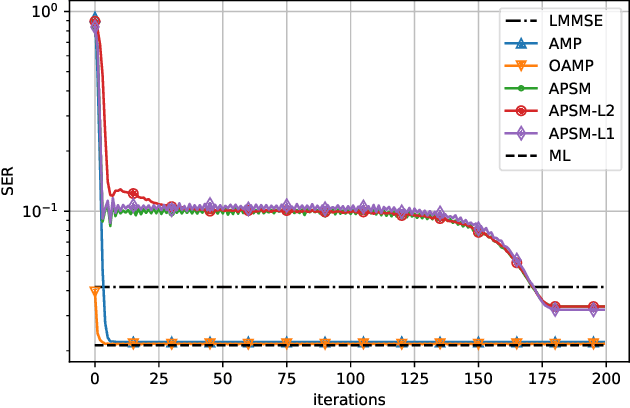
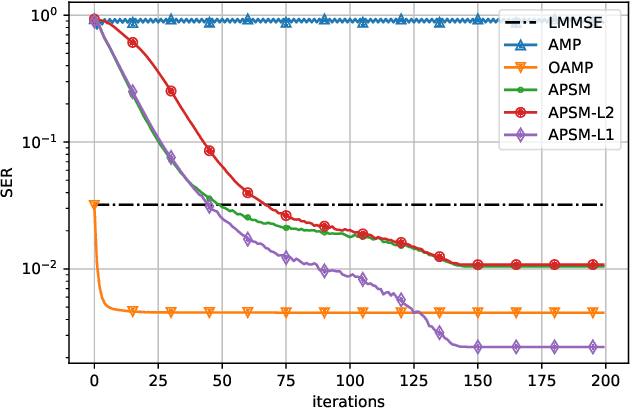
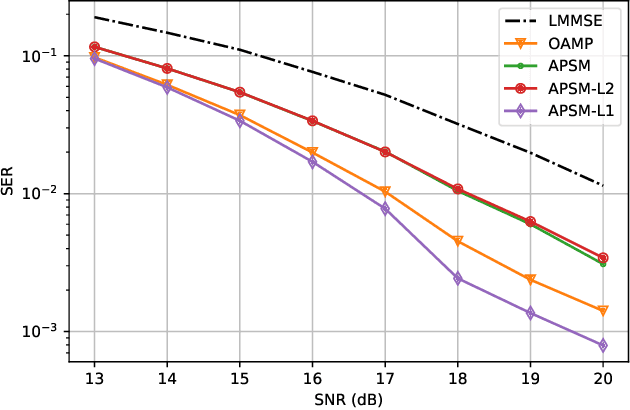
In this paper, we show that the adaptive projected subgradient method (APSM) is bounded perturbation resilient. To illustrate a potential application of this result, we propose a set-theoretic framework for MIMO detection, and we devise algorithms based on a superiorized APSM. Various low-complexity MIMO detection algorithms achieve excellent performance on i.i.d. Gaussian channels, but they typically incur high performance loss if realistic channel models are considered. Compared to existing low-complexity iterative detectors such as approximate message passing (AMP), the proposed algorithms can achieve considerably lower symbol error ratios over correlated channels. At the same time, the proposed methods do not require matrix inverses, and their complexity is similar to AMP.

Multi-Group Multicast Beamforming by Superiorized Projections onto Convex Sets

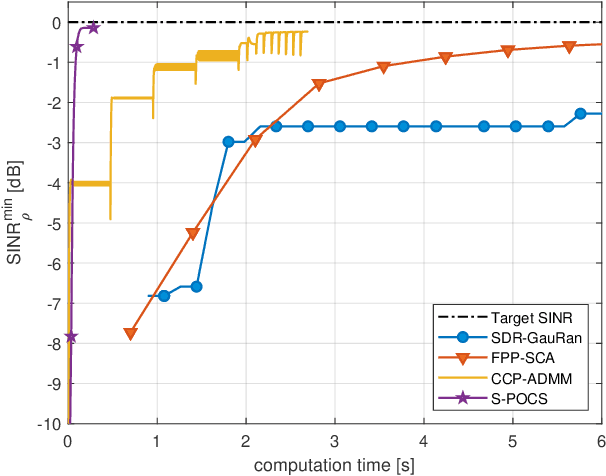
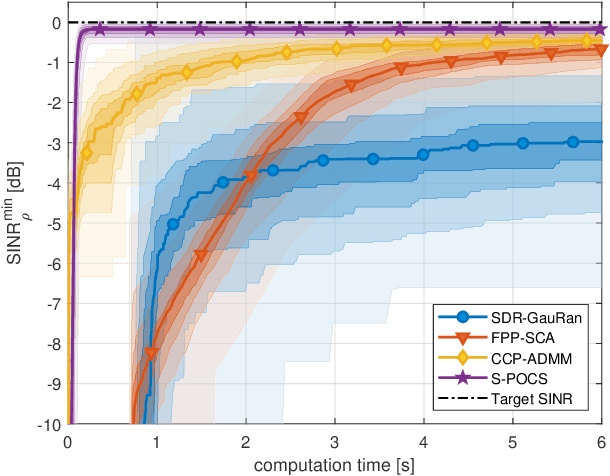
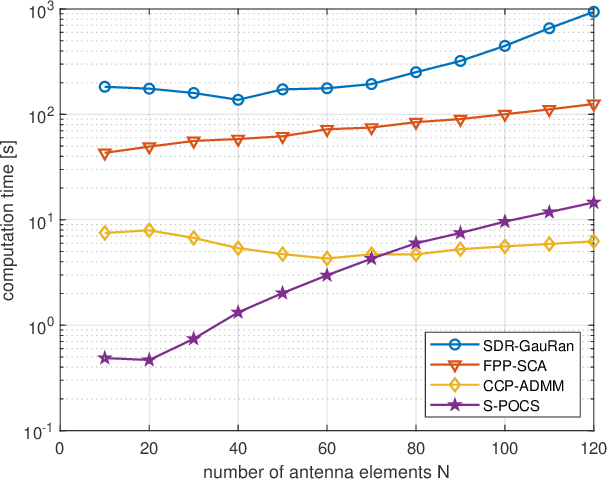
In this paper, we propose an iterative algorithm to address the nonconvex multi-group multicast beamforming problem with quality-of-service constraints and per-antenna power constraints. We formulate a convex relaxation of the problem as a semidefinite program in a real Hilbert space, which allows us to approximate a point in the feasible set by iteratively applying a bounded perturbation resilient fixed-point mapping. Inspired by the superiorization methodology, we use this mapping as a basic algorithm, and we add in each iteration a small perturbation with the intent to reduce the objective value and the distance to nonconvex rank-constraint sets. We prove that the sequence of perturbations is bounded, so the algorithm is guaranteed to converge to a feasible point of the relaxed semidefinite program. Simulations show that the proposed approach outperforms existing algorithms in terms of both computation time and approximation gap in many cases.