Multi-Group Multicast Beamforming by Superiorized Projections onto Convex Sets
Paper and Code
Feb 23, 2021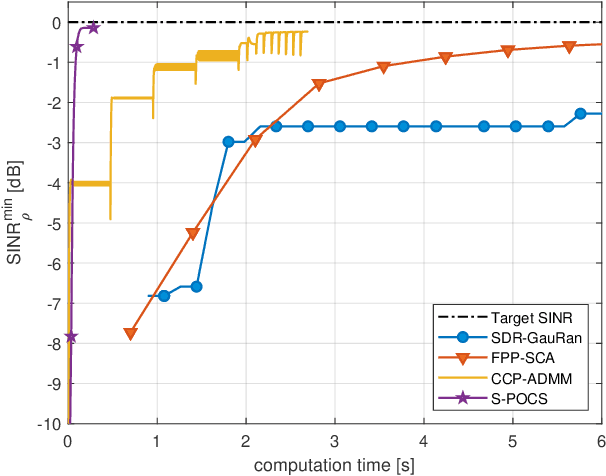
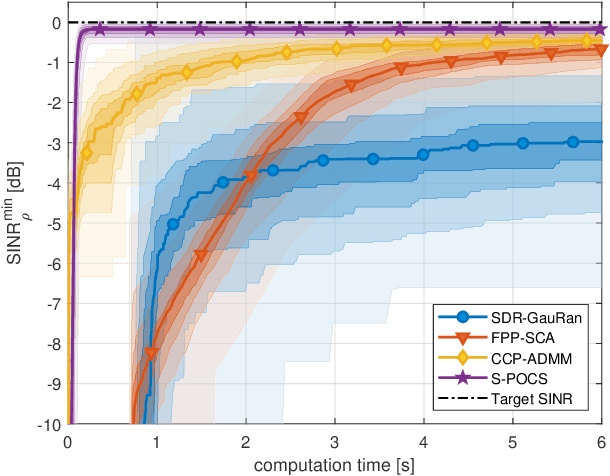

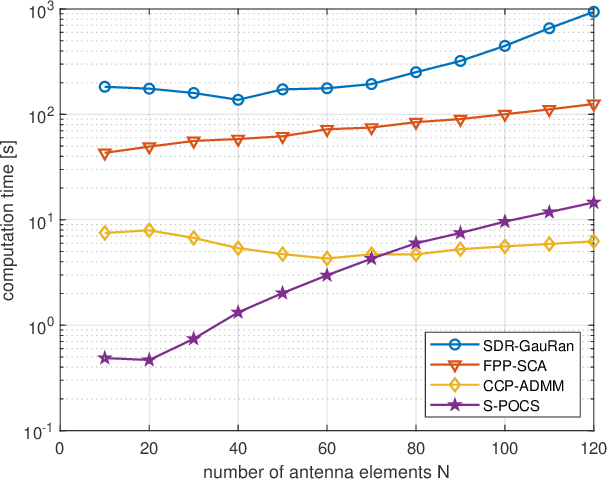
In this paper, we propose an iterative algorithm to address the nonconvex multi-group multicast beamforming problem with quality-of-service constraints and per-antenna power constraints. We formulate a convex relaxation of the problem as a semidefinite program in a real Hilbert space, which allows us to approximate a point in the feasible set by iteratively applying a bounded perturbation resilient fixed-point mapping. Inspired by the superiorization methodology, we use this mapping as a basic algorithm, and we add in each iteration a small perturbation with the intent to reduce the objective value and the distance to nonconvex rank-constraint sets. We prove that the sequence of perturbations is bounded, so the algorithm is guaranteed to converge to a feasible point of the relaxed semidefinite program. Simulations show that the proposed approach outperforms existing algorithms in terms of both computation time and approximation gap in many cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge