Joaquin Delgado Fernandez
Bridging Smart Meter Gaps: A Benchmark of Statistical, Machine Learning and Time Series Foundation Models for Data Imputation
Jan 13, 2025Abstract:The integrity of time series data in smart grids is often compromised by missing values due to sensor failures, transmission errors, or disruptions. Gaps in smart meter data can bias consumption analyses and hinder reliable predictions, causing technical and economic inefficiencies. As smart meter data grows in volume and complexity, conventional techniques struggle with its nonlinear and nonstationary patterns. In this context, Generative Artificial Intelligence offers promising solutions that may outperform traditional statistical methods. In this paper, we evaluate two general-purpose Large Language Models and five Time Series Foundation Models for smart meter data imputation, comparing them with conventional Machine Learning and statistical models. We introduce artificial gaps (30 minutes to one day) into an anonymized public dataset to test inference capabilities. Results show that Time Series Foundation Models, with their contextual understanding and pattern recognition, could significantly enhance imputation accuracy in certain cases. However, the trade-off between computational cost and performance gains remains a critical consideration.
Forecasting Anonymized Electricity Load Profiles
Jan 08, 2025


Abstract:In the evolving landscape of data privacy, the anonymization of electric load profiles has become a critical issue, especially with the enforcement of the General Data Protection Regulation (GDPR) in Europe. These electric load profiles, which are essential datasets in the energy industry, are classified as personal behavioral data, necessitating stringent protective measures. This article explores the implications of this classification, the importance of data anonymization, and the potential of forecasting using microaggregated data. The findings underscore that effective anonymization techniques, such as microaggregation, do not compromise the performance of forecasting models under certain conditions (i.e., forecasting aggregated). In such an aggregated level, microaggregated data maintains high levels of utility, with minimal impact on forecasting accuracy. The implications for the energy sector are profound, suggesting that privacy-preserving data practices can be integrated into smart metering technology applications without hindering their effectiveness.
Federated Learning: Organizational Opportunities, Challenges, and Adoption Strategies
Aug 04, 2023


Abstract:Restrictive rules for data sharing in many industries have led to the development of \ac{FL}. \ac{FL} is a \ac{ML} technique that allows distributed clients to train models collaboratively without the need to share their respective training data with others. In this article, we first explore the technical basics of FL and its potential applications. Second, we present a conceptual framework for the adoption of \ac{FL}, mapping organizations along the lines of their \ac{AI} capabilities and environment. We then discuss why exemplary organizations in different industries, including industry consortia, established banks, public authorities, and data-intensive SMEs might consider different approaches to \ac{FL}. To conclude, we argue that \ac{FL} presents an institutional shift with ample interdisciplinary research opportunities for the business and information systems engineering community.
Secure Federated Learning for Residential Short Term Load Forecasting
Nov 17, 2021
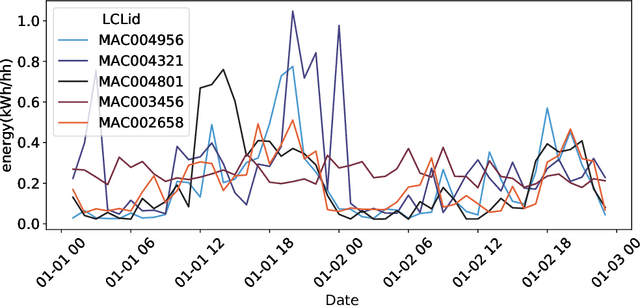
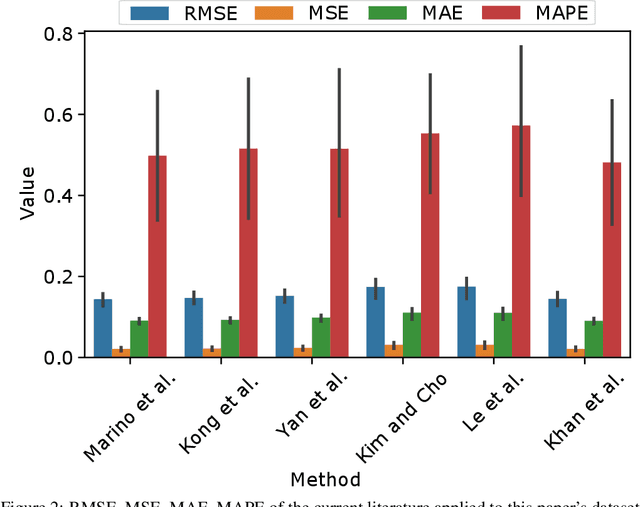

Abstract:The inclusion of intermittent and renewable energy sources has increased the importance of demand forecasting in power systems. Smart meters can play a critical role in demand forecasting due to the measurement granularity they provide. Consumers' privacy concerns, reluctance of utilities and vendors to share data with competitors or third parties, and regulatory constraints are some constraints smart meter forecasting faces. This paper examines a collaborative machine learning method for short-term demand forecasting using smart meter data as a solution to the previous constraints. Privacy preserving techniques and federated learning enable to ensure consumers' confidentiality concerning both, their data, the models generated using it (Differential Privacy), and the communication mean (Secure Aggregation). The methods evaluated take into account several scenarios that explore how traditional centralized approaches could be projected in the direction of a decentralized, collaborative and private system. The results obtained over the evaluations provided almost perfect privacy budgets (1.39,$10e^{-5}$) and (2.01,$10e^{-5}$) with a negligible performance compromise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge