Joan J. Cerdà
Spectral Ergodicity in Deep Learning Architectures via Surrogate Random Matrices
Jul 11, 2017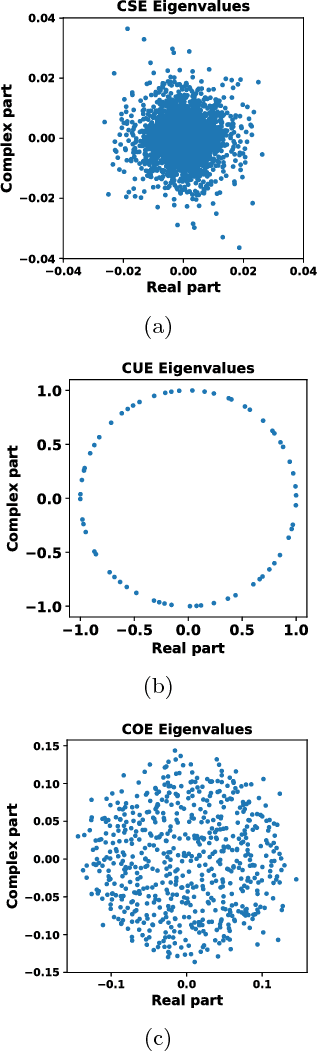
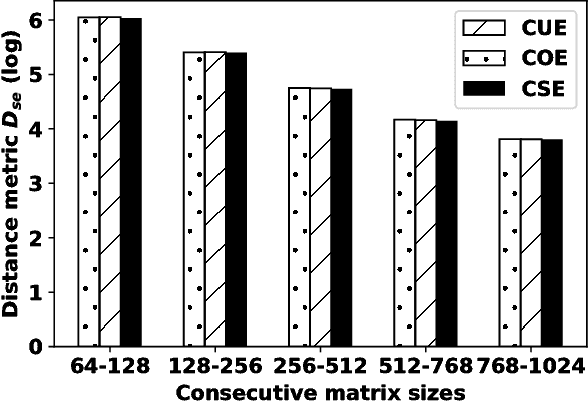
Abstract:In this work a novel method to quantify spectral ergodicity for random matrices is presented. The new methodology combines approaches rooted in the metrics of Thirumalai-Mountain (TM) and Kullbach-Leibler (KL) divergence. The method is applied to a general study of deep and recurrent neural networks via the analysis of random matrix ensembles mimicking typical weight matrices of those systems. In particular, we examine circular random matrix ensembles: circular unitary ensemble (CUE), circular orthogonal ensemble (COE), and circular symplectic ensemble (CSE). Eigenvalue spectra and spectral ergodicity are computed for those ensembles as a function of network size. It is observed that as the matrix size increases the level of spectral ergodicity of the ensemble rises, i.e., the eigenvalue spectra obtained for a single realisation at random from the ensemble is closer to the spectra obtained averaging over the whole ensemble. Based on previous results we conjecture that success of deep learning architectures is strongly bound to the concept of spectral ergodicity. The method to compute spectral ergodicity proposed in this work could be used to optimise the size and architecture of deep as well as recurrent neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge