Clustering to Minimize Cluster-Aware Norm Objectives

We initiate the study of the following general clustering problem. We seek to partition a given set $P$ of data points into $k$ clusters by finding a set $X$ of $k$ centers and assigning each data point to one of the centers. The cost of a cluster, represented by a center $x\in X$, is a monotone, symmetric norm $f$ (inner norm) of the vector of distances of points assigned to $x$. The goal is to minimize a norm $g$ (outer norm) of the vector of cluster costs. This problem, which we call $(f,g)$-Clustering, generalizes many fundamental clustering problems such as $k$-Center, $k$-Median , Min-Sum of Radii, and Min-Load $k$-Clustering . A recent line of research (Chakrabarty, Swamy [STOC'19]) studies norm objectives that are oblivious to the cluster structure such as $k$-Median and $k$-Center. In contrast, our problem models cluster-aware objectives including Min-Sum of Radii and Min-Load $k$-Clustering. Our main results are as follows. First, we design a constant-factor approximation algorithm for $(\textsf{top}_\ell,\mathcal{L}_1)$-Clustering where the inner norm ($\textsf{top}_\ell$) sums over the $\ell$ largest distances. Second, we design a constant-factor approximation\ for $(\mathcal{L}_\infty,\textsf{Ord})$-Clustering where the outer norm is a convex combination of $\textsf{top}_\ell$ norms (ordered weighted norm).

Parameterized Approximation for Robust Clustering in Discrete Geometric Spaces

We consider the well-studied Robust $(k, z)$-Clustering problem, which generalizes the classic $k$-Median, $k$-Means, and $k$-Center problems. Given a constant $z\ge 1$, the input to Robust $(k, z)$-Clustering is a set $P$ of $n$ weighted points in a metric space $(M,\delta)$ and a positive integer $k$. Further, each point belongs to one (or more) of the $m$ many different groups $S_1,S_2,\ldots,S_m$. Our goal is to find a set $X$ of $k$ centers such that $\max_{i \in [m]} \sum_{p \in S_i} w(p) \delta(p,X)^z$ is minimized. This problem arises in the domains of robust optimization [Anthony, Goyal, Gupta, Nagarajan, Math. Oper. Res. 2010] and in algorithmic fairness. For polynomial time computation, an approximation factor of $O(\log m/\log\log m)$ is known [Makarychev, Vakilian, COLT $2021$], which is tight under a plausible complexity assumption even in the line metrics. For FPT time, there is a $(3^z+\epsilon)$-approximation algorithm, which is tight under GAP-ETH [Goyal, Jaiswal, Inf. Proc. Letters, 2023]. Motivated by the tight lower bounds for general discrete metrics, we focus on \emph{geometric} spaces such as the (discrete) high-dimensional Euclidean setting and metrics of low doubling dimension, which play an important role in data analysis applications. First, for a universal constant $\eta_0 >0.0006$, we devise a $3^z(1-\eta_{0})$-factor FPT approximation algorithm for discrete high-dimensional Euclidean spaces thereby bypassing the lower bound for general metrics. We complement this result by showing that even the special case of $k$-Center in dimension $\Theta(\log n)$ is $(\sqrt{3/2}- o(1))$-hard to approximate for FPT algorithms. Finally, we complete the FPT approximation landscape by designing an FPT $(1+\epsilon)$-approximation scheme (EPAS) for the metric of sub-logarithmic doubling dimension.

Parameterized Approximation Schemes for Clustering with General Norm Objectives

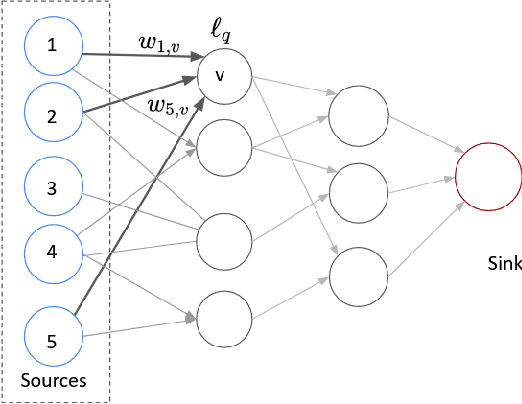
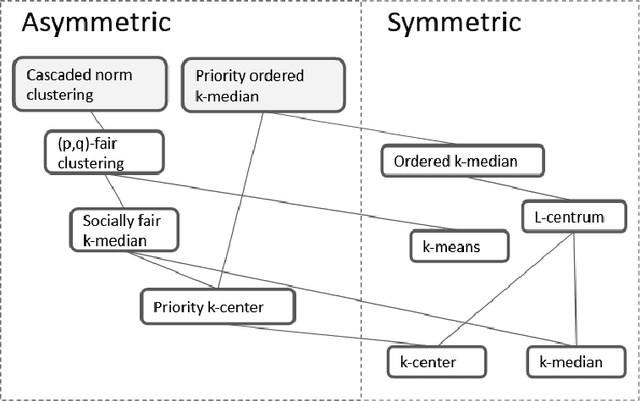
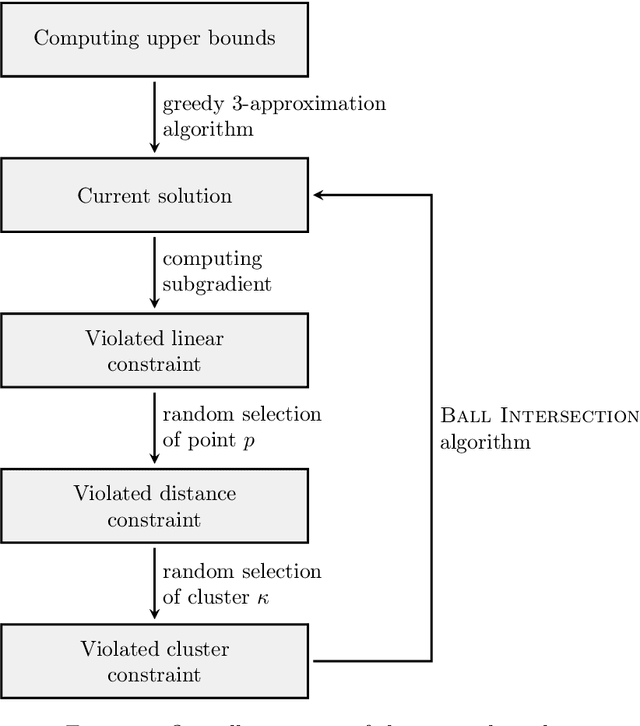
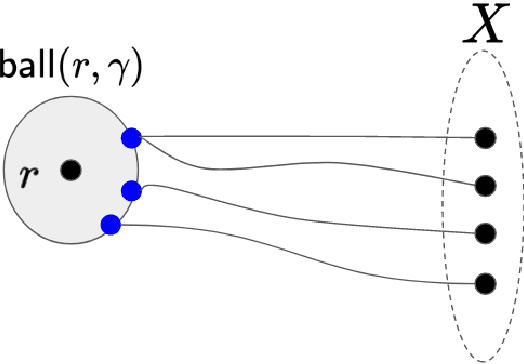
This paper considers the well-studied algorithmic regime of designing a $(1+\epsilon)$-approximation algorithm for a $k$-clustering problem that runs in time $f(k,\epsilon)poly(n)$ (sometimes called an efficient parameterized approximation scheme or EPAS for short). Notable results of this kind include EPASes in the high-dimensional Euclidean setting for $k$-center [Bad\u{o}iu, Har-Peled, Indyk; STOC'02] as well as $k$-median, and $k$-means [Kumar, Sabharwal, Sen; J. ACM 2010]. However, existing EPASes handle only basic objectives (such as $k$-center, $k$-median, and $k$-means) and are tailored to the specific objective and metric space. Our main contribution is a clean and simple EPAS that settles more than ten clustering problems (across multiple well-studied objectives as well as metric spaces) and unifies well-known EPASes. Our algorithm gives EPASes for a large variety of clustering objectives (for example, $k$-means, $k$-center, $k$-median, priority $k$-center, $\ell$-centrum, ordered $k$-median, socially fair $k$-median aka robust $k$-median, or more generally monotone norm $k$-clustering) and metric spaces (for example, continuous high-dimensional Euclidean spaces, metrics of bounded doubling dimension, bounded treewidth metrics, and planar metrics). Key to our approach is a new concept that we call bounded $\epsilon$-scatter dimension--an intrinsic complexity measure of a metric space that is a relaxation of the standard notion of bounded doubling dimension. Our main technical result shows that two conditions are essentially sufficient for our algorithm to yield an EPAS on the input metric $M$ for any clustering objective: (i) The objective is described by a monotone (not necessarily symmetric!) norm, and (ii) the $\epsilon$-scatter dimension of $M$ is upper bounded by a function of $\epsilon$.