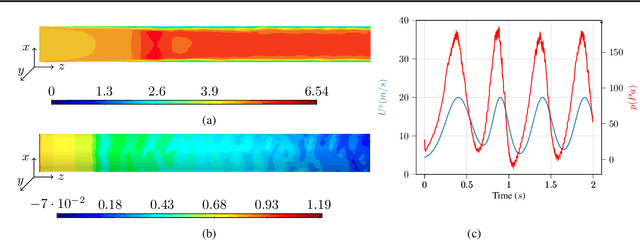
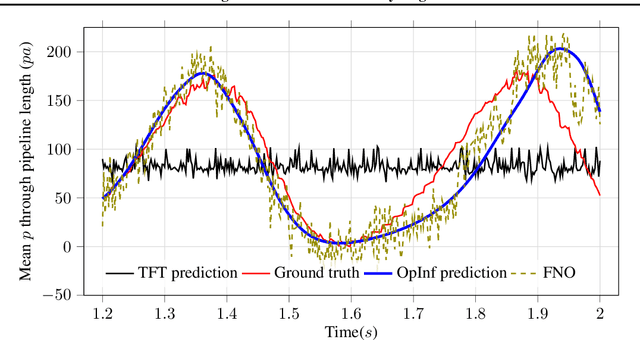
A Machine Learning Pressure Emulator for Hydrogen Embrittlement

A recent alternative for hydrogen transportation as a mixture with natural gas is blending it into natural gas pipelines. However, hydrogen embrittlement of material is a major concern for scientists and gas installation designers to avoid process failures. In this paper, we propose a physics-informed machine learning model to predict the gas pressure on the pipes' inner wall. Despite its high-fidelity results, the current PDE-based simulators are time- and computationally-demanding. Using simulation data, we train an ML model to predict the pressure on the pipelines' inner walls, which is a first step for pipeline system surveillance. We found that the physics-based method outperformed the purely data-driven method and satisfy the physical constraints of the gas flow system.

Non-Intrusive Reduced Models based on Operator Inference for Chaotic Systems

This work explores the physics-driven machine learning technique Operator Inference (OpInf) for predicting the state of chaotic dynamical systems. OpInf provides a non-intrusive approach to infer approximations of polynomial operators in reduced space without having access to the full order operators appearing in discretized models. Datasets for the physics systems are generated using conventional numerical solvers and then projected to a low-dimensional space via Principal Component Analysis (PCA). In latent space, a least-squares problem is set to fit a quadratic polynomial operator which is subsequently employed in a time-integration scheme in order to produce extrapolations in the same space. Once solved, the inverse PCA operation is applied for reconstructing the extrapolations in the original space. The quality of the OpInf predictions is assessed via the Normalized Root Mean Squared Error (NRMSE) metric from which the Valid Prediction Time (VPT) is computed. Numerical experiments considering the chaotic systems Lorenz 96 and the Kuramoto-Sivashinsky equation show promising forecasting capabilities of the OpInf reduced order models with VPT ranges that outperform state-of-the-art machine learning methods such as backpropagation and reservoir computing recurrent neural networks [1], as well as Markov neural operators [2]. The best results based on randomized initial conditions show that Lorenz 96 system can be forecasted up to 6.66 or 3.19 Lyapunov time units corresponding to the forcing terms F=8 and F=10, respectively, while the KS system achieved remarkable 794 Lyapunov time units.