HENet: Forcing a Network to Think More for Font Recognition

Although lots of progress were made in Text Recognition/OCR in recent years, the task of font recognition is remaining challenging. The main challenge lies in the subtle difference between these similar fonts, which is hard to distinguish. This paper proposes a novel font recognizer with a pluggable module solving the font recognition task. The pluggable module hides the most discriminative accessible features and forces the network to consider other complicated features to solve the hard examples of similar fonts, called HE Block. Compared with the available public font recognition systems, our proposed method does not require any interactions at the inference stage. Extensive experiments demonstrate that HENet achieves encouraging performance, including on character-level dataset Explor_all and word-level dataset AdobeVFR

Improving abcdSAT by At-Least-One Recently Used Clause Management Strategy

We improve further the 2015 version of abcdSAT by various heuristics such as at-least-one recently used strategy, learnt clause database approximation reduction etc. Based on the requirement of different tracks at the SAT Competition 2016, we develop three versions of abcdSAT: drup, inc and lim, which participate in the competition of main (agile), incremental library and no-limit track, respectively.

Improving SAT Solvers via Blocked Clause Decomposition

The decision variable selection policy used by the most competitive CDCL (Conflict-Driven Clause Learning) SAT solvers is either VSIDS (Variable State Independent Decaying Sum) or its variants such as exponential version EVSIDS. The common characteristic of VSIDS and its variants is to make use of statistical information in the solving process, but ignore structure information of the problem. For this reason, this paper modifies the decision variable selection policy, and presents a SAT solving technique based on BCD (Blocked Clause Decomposition). Its basic idea is that a part of decision variables are selected by VSIDS heuristic, while another part of decision variables are selected by blocked sets that are obtained by BCD. Compared with the existing BCD-based technique, our technique is simple, and need not to reencode CNF formulas. SAT solvers for certified UNSAT track can apply also our BCD-based technique. Our experiments on application benchmarks demonstrate that the new variables selection policy based on BCD can increase the performance of SAT solvers such as abcdSAT. The solver with BCD solved an instance from the SAT Race 2015 that was not solved by any solver so far. This shows that in some cases, the heuristic based on structure information is more efficient than that based on statistical information.

A Dynamic Phase Selection Strategy for Satisfiability Solvers

The phase selection is an important of a SAT Solver based on conflict-driven DPLL. This paper presents a new phase selection strategy, in which the weight of each literal is defined as the sum of its implied-literals static weights. The implied literals of each literal is computed dynamically during the search. Therefore, it is call a dynamic phase selection strategy. In general, computing dynamically a weight is time-consuming. Hence, so far no SAT solver applies successfully a dynamic phase selection. Since the implied literal of our strategy conforms to that of the search process, the usual two watched-literals scheme can be applied here. Thus, the cost of our dynamic phase selection is very low. To improve Glucose 2.0 which won a Gold Medal for application category at SAT 2011 competition, we build five phase selection schemes using the dynamic phase selection policy. On application instances of SAT 2011, Glucose improved by the dynamic phase selection is significantly better than the original Glucose. We conduct also experiments on Lingeling, using the dynamic phase selection policy, and build two phase selection schemes. Experimental results show that the improved Lingeling is better than the original Lingeling.

Solving Rubik's Cube Using SAT Solvers

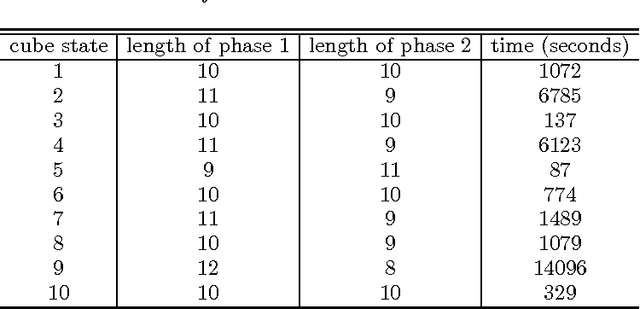
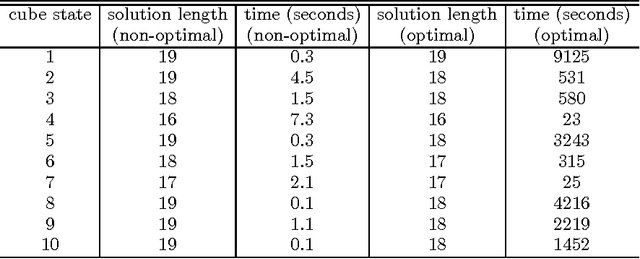
Rubik's Cube is an easily-understood puzzle, which is originally called the "magic cube". It is a well-known planning problem, which has been studied for a long time. Yet many simple properties remain unknown. This paper studies whether modern SAT solvers are applicable to this puzzle. To our best knowledge, we are the first to translate Rubik's Cube to a SAT problem. To reduce the number of variables and clauses needed for the encoding, we replace a naive approach of 6 Boolean variables to represent each color on each facelet with a new approach of 3 or 2 Boolean variables. In order to be able to solve quickly Rubik's Cube, we replace the direct encoding of 18 turns with the layer encoding of 18-subtype turns based on 6-type turns. To speed up the solving further, we encode some properties of two-phase algorithm as an additional constraint, and restrict some move sequences by adding some constraint clauses. Using only efficient encoding cannot solve this puzzle. For this reason, we improve the existing SAT solvers, and develop a new SAT solver based on PrecoSAT, though it is suited only for Rubik's Cube. The new SAT solver replaces the lookahead solving strategy with an ALO (\emph{at-least-one}) solving strategy, and decomposes the original problem into sub-problems. Each sub-problem is solved by PrecoSAT. The empirical results demonstrate both our SAT translation and new solving technique are efficient. Without the efficient SAT encoding and the new solving technique, Rubik's Cube will not be able to be solved still by any SAT solver. Using the improved SAT solver, we can find always a solution of length 20 in a reasonable time. Although our solver is slower than Kociemba's algorithm using lookup tables, but does not require a huge lookup table.