Jian Qing Shi
Intrinsic Wrapped Gaussian Process Regression Modeling for Manifold-valued Response Variable
Nov 28, 2024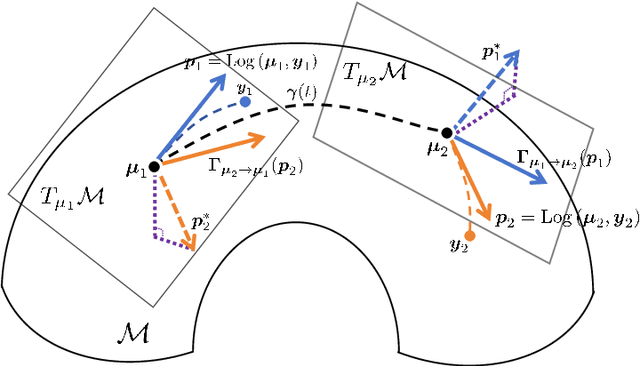
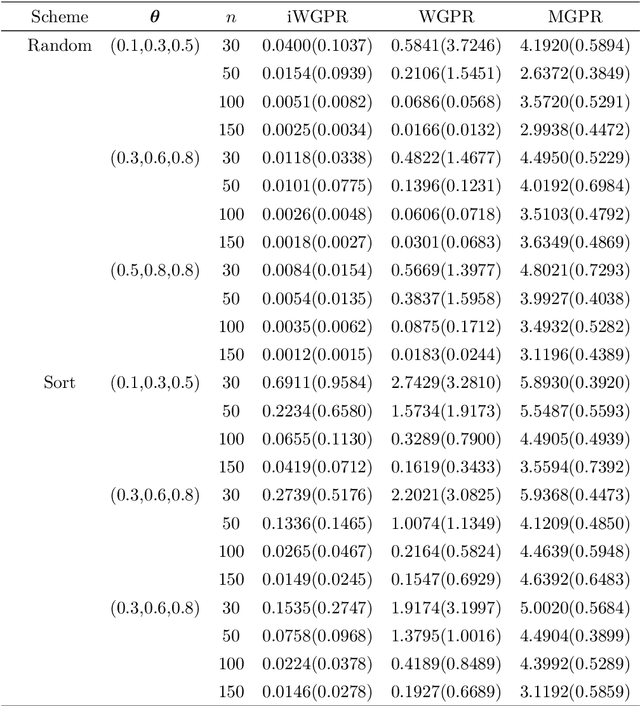
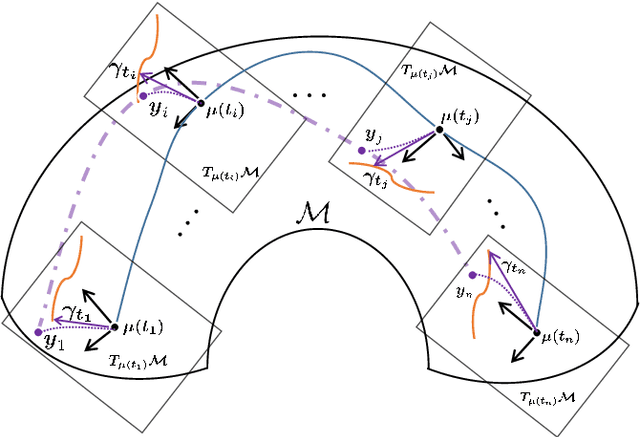
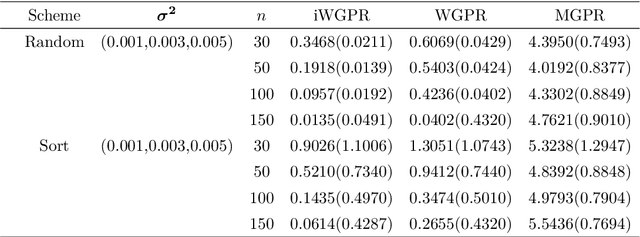
Abstract:In this paper, we propose a novel intrinsic wrapped Gaussian process regression model for response variable measured on Riemannian manifold. We apply the parallel transport operator to define an intrinsic covariance structure addressing a critical aspect of constructing a well defined Gaussian process regression model. We show that the posterior distribution of regression function is invariant to the choice of orthonormal frames for the coordinate representations of the covariance function. This method can be applied to data situated not only on Euclidean submanifolds but also on manifolds without a natural ambient space. The asymptotic properties for estimating the posterior distribution is established. Numerical studies, including simulation and real-world examples, indicate that the proposed method delivers strong performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge