TinySeg: Model Optimizing Framework for Image Segmentation on Tiny Embedded Systems

Image segmentation is one of the major computer vision tasks, which is applicable in a variety of domains, such as autonomous navigation of an unmanned aerial vehicle. However, image segmentation cannot easily materialize on tiny embedded systems because image segmentation models generally have high peak memory usage due to their architectural characteristics. This work finds that image segmentation models unnecessarily require large memory space with an existing tiny machine learning framework. That is, the existing framework cannot effectively manage the memory space for the image segmentation models. This work proposes TinySeg, a new model optimizing framework that enables memory-efficient image segmentation for tiny embedded systems. TinySeg analyzes the lifetimes of tensors in the target model and identifies long-living tensors. Then, TinySeg optimizes the memory usage of the target model mainly with two methods: (i) tensor spilling into local or remote storage and (ii) fused fetching of spilled tensors. This work implements TinySeg on top of the existing tiny machine learning framework and demonstrates that TinySeg can reduce the peak memory usage of an image segmentation model by 39.3% for tiny embedded systems.

The Geometry of Nonlinear Embeddings in Kernel Discriminant Analysis

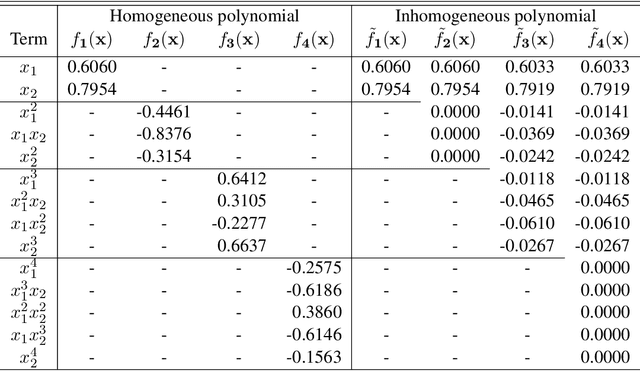
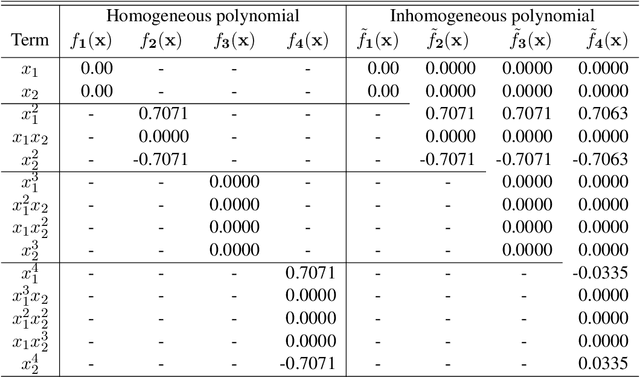
Fisher's linear discriminant analysis is a classical method for classification, yet it is limited to capturing linear features only. Kernel discriminant analysis as an extension is known to successfully alleviate the limitation through a nonlinear feature mapping. We study the geometry of nonlinear embeddings in discriminant analysis with polynomial kernels and Gaussian kernel by identifying the population-level discriminant function that depends on the data distribution and the kernel. In order to obtain the discriminant function, we solve a generalized eigenvalue problem with between-class and within-class covariance operators. The polynomial discriminants are shown to capture the class difference through the population moments explicitly. For approximation of the Gaussian discriminant, we use a particular representation of the Gaussian kernel by utilizing the exponential generating function for Hermite polynomials. We also show that the Gaussian discriminant can be approximated using randomized projections of the data. Our results illuminate how the data distribution and the kernel interact in determination of the nonlinear embedding for discrimination, and provide a guideline for choice of the kernel and its parameters.