Jerome Monnot
Computing and Testing Pareto Optimal Committees
Mar 18, 2018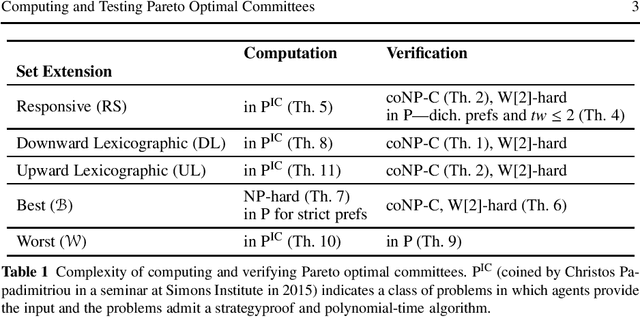
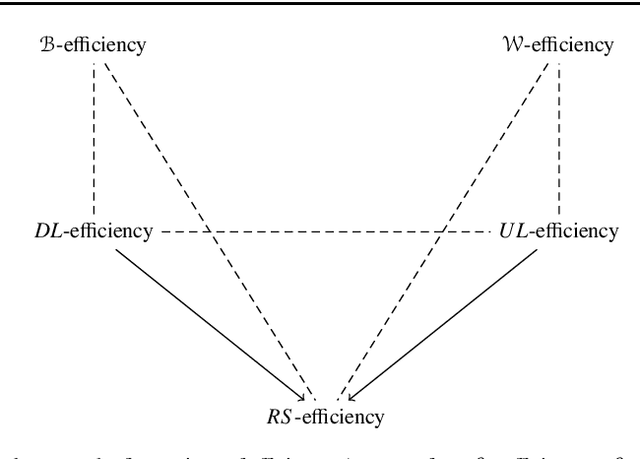
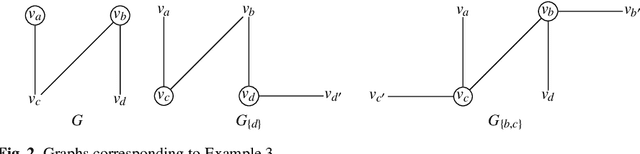
Abstract:Selecting a set of alternatives based on the preferences of agents is an important problem in committee selection and beyond. Among the various criteria put forth for the desirability of a committee, Pareto optimality is a minimal and important requirement. As asking agents to specify their preferences over exponentially many subsets of alternatives is practically infeasible, we assume that each agent specifies a weak order on single alternatives, from which a preference relation over subsets is derived using some preference extension. We consider five prominent extensions (responsive, downward lexicographic, upward lexicographic, best, and worst). For each of them, we consider the corresponding Pareto optimality notion, and we study the complexity of computing and verifying Pareto optimal outcomes. We also consider strategic issues: for four of the set extensions, we present a linear-time, Pareto optimal and strategyproof algorithm that even works for weak preferences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge